Опять неравенство в C[0,1]

[Ian]

Пришла видимо из задачника
Найти наименьшее М, что для любой дважды непрерывно дифференцируемой действительной [math]x(t)
[math]\max_{[0,1]}|x'(t)|\leq M\left(\max_{[0,1]}|x(t)|+\max_{[0,1]}|x''(t)|\right)
Несколько соображений. Изменяя [math]x(t) на константу, можно считать, что 0 попадет в середину области значений [math]x(t), тогда второй максимум наименьший, остальные не меняются.Тогда можем считать, что [math]x(0,5)=0 и [math]x(t)<0левее этой точки и график центрально-симметричен относительно середины отрезка( если на одной половине отрезка функция хороша, а на другой не так хороша, то что нам мешает взять ее центрально-симметричной. Только разрыв второй производной, но его легко сгладить с минимальными изменениями для неравенства. Далее, возможно, наихудшая функция среди решений уравнения
[math]x'=\pm M(x+x'') , а так как для [math]x(t)=2t-1 [math]M=2, то M>2 и все решения тут комплексные экспоненты.
Но какой-то сложный счет получается

[Ian]

Получилось, что [math]C(2t-1) и есть экстремальная функция и [math]M=2
Предположим, [math]x'_{max}=1 в точке [math]t=\tau, а также [math]|x''|\leq d тогда
[math]x(1)\geq x(\tau)+(1-\tau)-\frac d2(1-\tau)^2
[math]x(0)\leq x(\tau)-\tau+\frac d2\tau ^2
Вычитаем
[math]\max_{[0,1]}|x(t)|\geq \frac 12(x(1)-x(0))\geq \frac 12(1-\frac d2(2\tau^2-2\tau+1))\geq \frac 12-\frac d4
[math]\max_{[0,1]}|x(t)|+d\geq \frac 12+\frac {3d}4\geq \frac 12, а для М=2 есть пример

[zykov]

Да, верно.
Если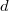 большое - 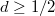, то 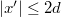, т.к. 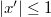по выбору.
Если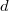 маленькое - 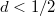, то достаточно оценки параболами.