Дискретное распределение почти без памяти
Дискретное распределение почти без памяти
Случайная величина обладает свойством [math].Найти ее функцию распределения.
Конечно, годится экспоненциальное, оно "без памяти", вероятность, что отказ не случится в промежуток длины T, если до этого не случился -постоянна. Но есть и дискретные распределения с таким свойством, экзотические какие-то. Только я даже матожидание их не могу элементарно посчитать.
Дискретное распределение почти без памяти
Я так понимаю, что если  , то
, то  .
.
Значит для любого выбранного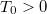 можно на
можно на 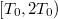 определить как угодно
определить как угодно 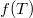 (можно разрывно), так чтобы она не возрастала,
(можно разрывно), так чтобы она не возрастала,  и
и  .
.
Это однозначно определит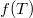 для всех
для всех 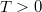 (с дельта-функциями плотности в местах разрывов).
(с дельта-функциями плотности в местах разрывов).
На бесконечности оно будет экспоненциально убывать. В нуле будет стремится к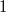 .
.
Значит для любого выбранного
Это однозначно определит
На бесконечности оно будет экспоненциально убывать. В нуле будет стремится к
Дискретное распределение почти без памяти
Да, а самым трудным оказалось доказательство, что [math], то есть что носитель СВ на положительной полуоси. Если бы для [math] равенство было задано, то [math] но и тогда почему [math]. И тут я вспомнил, что условная вероятность просто не определена при условии того, вероятность чего 0.
Теперь, если [math], [math], то чему же равно q? (
Теперь, если [math], [math], то чему же равно q? (
Дискретное распределение почти без памяти
Если для определенности выбрать 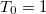 и задать
и задать 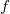 на
на 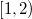 , то матожидание можно посчитать так:
, то матожидание можно посчитать так:
![$$E[T]=-\int_0^{+\infty} t f'(t) \; dt = -\sum_{n=-\infty}^{+\infty} \int_{2^n}^{2^{n+1}} t f'(t) \; dt = -\sum_{n=-\infty}^{+\infty} \int_1^2 2^{n+1} t f'(2^n t) \; dt =$$ $$E[T]=-\int_0^{+\infty} t f'(t) \; dt = -\sum_{n=-\infty}^{+\infty} \int_{2^n}^{2^{n+1}} t f'(t) \; dt = -\sum_{n=-\infty}^{+\infty} \int_1^2 2^{n+1} t f'(2^n t) \; dt =$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24E%5BT%5D%3D-%5Cint_0%5E%7B%2B%5Cinfty%7D%20t%20f%27%28t%29%20%5C%3B%20dt%20%3D%20-%5Csum_%7Bn%3D-%5Cinfty%7D%5E%7B%2B%5Cinfty%7D%20%5Cint_%7B2%5En%7D%5E%7B2%5E%7Bn%2B1%7D%7D%20t%20f%27%28t%29%20%5C%3B%20dt%20%3D%0A-%5Csum_%7Bn%3D-%5Cinfty%7D%5E%7B%2B%5Cinfty%7D%20%5Cint_1%5E2%202%5E%7Bn%2B1%7D%20t%20f%27%282%5En%20t%29%20%5C%3B%20dt%20%3D%24%24)
![$$= -\sum_{n=-\infty}^{+\infty} \int_1^2 2^{n+1} t f^{2^n-1}(t) f'(t) \; dt = -\int_1^2 [\sum_{n=-\infty}^{+\infty} 2^{n+1} f^{2^n-1}(t)] \; t f'(t) \; dt = -\int_1^2 t \; g(f(t)) \; f'(t) \; dt$$ $$= -\sum_{n=-\infty}^{+\infty} \int_1^2 2^{n+1} t f^{2^n-1}(t) f'(t) \; dt = -\int_1^2 [\sum_{n=-\infty}^{+\infty} 2^{n+1} f^{2^n-1}(t)] \; t f'(t) \; dt = -\int_1^2 t \; g(f(t)) \; f'(t) \; dt$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%3D%20-%5Csum_%7Bn%3D-%5Cinfty%7D%5E%7B%2B%5Cinfty%7D%20%5Cint_1%5E2%202%5E%7Bn%2B1%7D%20t%20f%5E%7B2%5En-1%7D%28t%29%20f%27%28t%29%20%5C%3B%20dt%20%3D%0A-%5Cint_1%5E2%20%5B%5Csum_%7Bn%3D-%5Cinfty%7D%5E%7B%2B%5Cinfty%7D%202%5E%7Bn%2B1%7D%20f%5E%7B2%5En-1%7D%28t%29%5D%20%5C%3B%20t%20f%27%28t%29%20%5C%3B%20dt%20%3D%0A-%5Cint_1%5E2%20t%20%5C%3B%20g%28f%28t%29%29%20%5C%3B%20f%27%28t%29%20%5C%3B%20dt%24%24)
Так что при
при 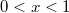 .
.
Что-то Вольфрам эту сумму не берет...
Так что
Что-то Вольфрам эту сумму не берет...
Последний раз редактировалось zykov 15 май 2020, 14:35, всего редактировалось 1 раз.
Дискретное распределение почти без памяти
Ian писал(а):Source of the post то чему же равно q?
Любому числу более 0, менее 1.
Дискретное распределение почти без памяти
Последний раз редактировалось zykov 15 май 2020, 14:36, всего редактировалось 1 раз.
Дискретное распределение почти без памяти
Вот график ![$E[T]$ $E[T]$](http://fx.ifz.ru/tex2.php?d=120&i=%24E%5BT%5D%24) от
от 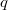 :
:
(Суммирование было от -50 до 50, этого достаточно - далее хвосты очень маленькие.)
(Суммирование было от -50 до 50, этого достаточно - далее хвосты очень маленькие.)
Дискретное распределение почти без памяти
Согласен, вопрос был дурацкий.zykov писал(а):Ian писал(а):Source of the post то чему же равно q?
Любому числу более 0, менее 1.
....
Но при малых q матожидание должно быть очень мало, очевидно? А где это на графике?
Дискретное распределение почти без памяти
Ian писал(а):Source of the post Но при малых q матожидание должно быть очень мало
Там в
Из-за этого при малых
Ведь
Дискретное распределение почти без памяти
Да, чего-то у меня не сходится. Где-то напутал наверно.
Вот посчитал напрямую для дискретного случая:

UPD: исправил сумму
Вот посчитал напрямую для дискретного случая:
UPD: исправил сумму
Последний раз редактировалось zykov 15 май 2020, 23:55, всего редактировалось 1 раз.
Дискретное распределение почти без памяти
У меня было [math]
Преобразование Абеля:
[math]
эта функция неэлементарная. возрастающая при [math] , численный расчет дает [math]
Преобразование Абеля:
[math]
эта функция неэлементарная. возрастающая при [math] , численный расчет дает [math]
Дискретное распределение почти без памяти
Да, так и получается.
Вот кстати в непрерывном случае, если распределение экспоненциальное и выбрать так же параметр , то матожидание будет
, то матожидание будет ![$E[T] = -\frac{1}{\log q}$ $E[T] = -\frac{1}{\log q}$](http://fx.ifz.ru/tex2.php?d=120&i=%24E%5BT%5D%20%3D%20-%5Cfrac%7B1%7D%7B%5Clog%20q%7D%24) .
.
Вот график:
Вот кстати в непрерывном случае, если распределение экспоненциальное и выбрать так же параметр
Вот график:
Дискретное распределение почти без памяти
Вот забавный график - отношение матожидания для дискретного случая к матожиданию экспоненциального распределения, т.е. упомянутая выше сумма умноженная на  :
:
Т.е. относительные отклонения имеют малый порядок около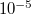 , довольно стабильную амплитуду, частота колебаний растёт по мере приближения к 1.
, довольно стабильную амплитуду, частота колебаний растёт по мере приближения к 1.
Причина осциляций видимо в том, что график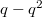 имеет максимум при
имеет максимум при 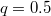 . По мере того как мы меняем
. По мере того как мы меняем 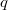 этот максимум (точнее один из
этот максимум (точнее один из 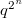 ) то попадает на целое
) то попадает на целое  , то оказывается между целыми.
, то оказывается между целыми.
UPD:
Т.е. относительные отклонения имеют малый порядок около
Причина осциляций видимо в том, что график
UPD:
Последний раз редактировалось zykov 16 май 2020, 07:23, всего редактировалось 1 раз.
Дискретное распределение почти без памяти
zykov писал(а):Source of the post то попадает на целое, то оказывается между целыми
Вот график
Похоже на фазу этих колебаний.
Дискретное распределение почти без памяти
zykov писал(а):Source of the post Причина осциляций видимо в том
Собственно, если рассмотреть функцию
Т.е. например достаточно обсчитать
Это же даст периодичность
Дискретное распределение почти без памяти
Для 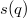 получается такая аппроксимация:
получается такая аппроксимация:
 .
.
Примерно и
и  .
.
Относительная ошибка около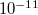 .
.
UPD: Следующая гармоника .
.
Примерно и
и  .
.
Дальше только ошибки округления (double float числа имеют точность около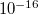 ).
).
Примерно
Относительная ошибка около
UPD: Следующая гармоника
Примерно
Дальше только ошибки округления (double float числа имеют точность около
Последний раз редактировалось zykov 16 май 2020, 14:50, всего редактировалось 4 раз.
Дискретное распределение почти без памяти
Интересно, что амплитуды гармоник так быстро убывают...
Дискретное распределение почти без памяти
Теперь можно оправдать название " распределение почти без памяти". Можно характеризовать случайную величину интегральной функцией распределения [math], а можно и введенной нами [math], между ними соотношение [math], но [math] только на дискретном множестве. Зафиксируем [math], тогда можно утверждать, что график [math]- распределения без памяти - можно накрыть системой прямоугольников, два угла каждого на графике, а проекции на ось [math] и тп. Тогда будет накрыт и график любой [math], удовлетворяющей условию задачи, и при взгляде издали -распределения близки. Что можно использовать при испытаниях на отказ, для N испытываемых элементов проверять, сколько отказало через 1сек; 2сек; 4 сек; ...65536 сек;...- а остальное время не волноваться. Тогда. если распределение моментов отказа будет близко к найденному - делаем вывод, что оно "почти без памяти", то есть отказ связан не с усталостью комплектующих, а со случайными факторами.
Дискретное распределение почти без памяти
Тут немного напутал. Для непрерывного случая должно быть так:
Например если
Дискретное распределение почти без памяти
Насчёт того, почему два логарифма по базе 2.
Потому что внешний логарифм соответствует
Для внутреннего логарифма выбор базы ещё менее важен. Другая база просто даст сдвиг по фазе, т.е. просто другую точку отсчёта. Но база 2 немного удобнее, т.к. тогда для
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость