Определитель вроде Вандермонда
Определитель вроде Вандермонда
Пусть [math] произвольные действительные числа. Определим элементы матрицы nxn
[math]
Чему равен определитель матрицы А?
Так как [math] полином степени j от [math],то весь определитель - полином степени [math] от [math] антисимметричный, то есть меняющий знак при нечетной перестановке чисел [math] и не меняющийся при четной. Отсюда [math] сомножителей в этом многочлене известны [math] и остается один сомножитель степени n, симметричный, значит выражающийся через симметричные полиномы от [math], то есть через коэффициенты по t уравнения [math]. Только выяснить как и доказать
[math]
Чему равен определитель матрицы А?
Так как [math] полином степени j от [math],то весь определитель - полином степени [math] от [math] антисимметричный, то есть меняющий знак при нечетной перестановке чисел [math] и не меняющийся при четной. Отсюда [math] сомножителей в этом многочлене известны [math] и остается один сомножитель степени n, симметричный, значит выражающийся через симметричные полиномы от [math], то есть через коэффициенты по t уравнения [math]. Только выяснить как и доказать
Последний раз редактировалось Ian 29 апр 2020, 11:54, всего редактировалось 1 раз.
Определитель вроде Вандермонда
Ian писал(а):Source of the post Так как cos(jx) полином степени j от cosx,
Да, это полиномы Чебышева первого рода:
Если
Вот например:
Определитель вроде Вандермонда
А как считали для n=4? Что-то Вы быстро, вот у меня лежит расчет этого определителя на 10ти страницах. Хотите через файлообменник передам, там рукописно много мег Но результаты совпали так что респект
Определитель вроде Вандермонда
Ian писал(а):Source of the post А как считали для n=4?
Да за меня Maxima считала.
Задал матрицу "m4" руками с полиномами Чебышева. А там команда "determinant(m4),factor" выдаёт это выражение.
Определитель вроде Вандермонда
А для 5ти?
Если обозначить
[math], то это довольно близко к P(-1/2) Почему-то)
Ой. еще ближе к [math]
Если обозначить
[math], то это довольно близко к P(-1/2) Почему-то)
Ой. еще ближе к [math]
Последний раз редактировалось Ian 29 апр 2020, 12:03, всего редактировалось 2 раз.
Определитель вроде Вандермонда
Вобщем всё это похоже на детерминант Вандермонда.
Только там с 0-ой степени начинается, а у Вас с 1-ой.
Если у Вас тоже сделать с 0-ой степени -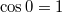 , то тоже будет детерминант Вандермонда умноженный на
, то тоже будет детерминант Вандермонда умноженный на 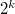 , где
, где 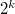 равно произведению старших коэффициентов в полиномах Чебышева. Т.е.
равно произведению старших коэффициентов в полиномах Чебышева. Т.е. 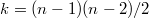 .
.
А Ваш детерминант - это один из миноров этого детерминанта (минор при последней "1" в первом столбце).
Только там с 0-ой степени начинается, а у Вас с 1-ой.
Если у Вас тоже сделать с 0-ой степени -
А Ваш детерминант - это один из миноров этого детерминанта (минор при последней "1" в первом столбце).
Последний раз редактировалось zykov 29 апр 2020, 14:48, всего редактировалось 3 раз.
Определитель вроде Вандермонда
Да при [math] хоть бы получить. И он не мой)
Определитель вроде Вандермонда
Если 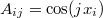 , где
, где 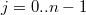 , то
, то 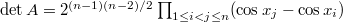 .
.
Определитель вроде Вандермонда
Но это совсем не то что будет при [math]. Красиво и просто, но чем поможет
Определитель вроде Вандермонда
Если мы начинаем с 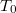 , то получается определитель Вандермонда, потому что мы можем привести матрицу к матрице Вандермонда.
, то получается определитель Вандермонда, потому что мы можем привести матрицу к матрице Вандермонда.
Первая строка и так везде 1. Вторая строка и так везде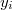 . В третьей строке многчлен второй степени. Но мы можем к ней добавить первую строку (операция не меняет определитель), остается только
. В третьей строке многчлен второй степени. Но мы можем к ней добавить первую строку (операция не меняет определитель), остается только 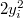 .
.
И так далее, в каждой строке от многочлена останется только старшее слагаемое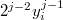 . Отсюда и определитель равен определителю Вандермонда умноженному на
. Отсюда и определитель равен определителю Вандермонда умноженному на 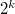 .
.
Если мы начинаем с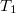 , то в нечётных строках мы так же можем привести многочлен к такому же виду - только страшее слагаемое.
, то в нечётных строках мы так же можем привести многочлен к такому же виду - только страшее слагаемое.
В чётных строках мы тоже сможем занулить почти все слагаемые. Но кроме старшего слагаемого останется ещё нулевой порядок (во второй строке "-1", в четвертой "-3", в шестой "-10", в восьмой "-35" и т.д.)
Остается только всё это посчитать...
Первая строка и так везде 1. Вторая строка и так везде
И так далее, в каждой строке от многочлена останется только старшее слагаемое
Если мы начинаем с
В чётных строках мы тоже сможем занулить почти все слагаемые. Но кроме старшего слагаемого останется ещё нулевой порядок (во второй строке "-1", в четвертой "-3", в шестой "-10", в восьмой "-35" и т.д.)
Остается только всё это посчитать...
Определитель вроде Вандермонда
А если например для n=4 положить [math] равным корням 4-й степени из 3 (четырем разным комплексным), что это нам скажет о значении искомого сомножителя. Ну точнее не из 3 а из того, что обращает строчку в 0 -константа находится
Определитель вроде Вандермонда
А откуда взялась задача?
Может всё-таки должно быть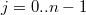 , а не
, а не 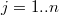 ?
?
Может всё-таки должно быть
Определитель вроде Вандермонда
У последней системы надо доказать существование положительного решения. И у подобных. Для этого главный определитель хорошо бы иметь явно.
Определитель вроде Вандермонда
Там вроде более конкретная матрица возникает 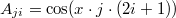 .
.
Определитель вроде Вандермонда
Честно говоря, не вижу как формула для определителя поможет доказать положительность решений линейной системы.
Попробовал посчитать - действительно для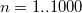 и
и 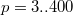 решения получаются положительные.
решения получаются положительные.
Но оказалось, что любой туда не подставить - это просто неверно. Там должен быть именно такой
туда не подставить - это просто неверно. Там должен быть именно такой 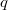 (
(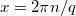 ). Если например вместо
). Если например вместо 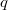 подставить
подставить 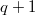 , то возникают отрицательные решения при
, то возникают отрицательные решения при 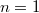 . А если подставить
. А если подставить 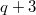 , то и при
, то и при 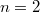 тоже будут отрицательные.
тоже будут отрицательные.
Попробовал посчитать - действительно для
Но оказалось, что любой
Определитель вроде Вандермонда
Вообще это преобразование похоже на Discrete cosine transform (DCT-II).
Только в фазе есть дополнительный множитель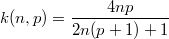 , который меняется в пределах от
, который меняется в пределах от 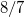 до
до 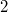 (не доходя до
(не доходя до 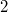 ).
).
Только в фазе есть дополнительный множитель
Определитель вроде Вандермонда
При больших  и
и 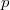 решение выглядит примерно так:
решение выглядит примерно так:
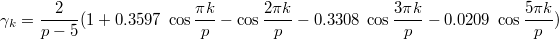
Есть и другие гармоники (в основном нечётные), но с меньшим весом.
Эта аппроксимация в целом положительная. Только в конце немного заходит в минус.
Наверно неравенство при и
и 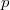 более какого-то порога можно дожать такми путём, выстраивая цепочку неравенств. Правда для
более какого-то порога можно дожать такми путём, выстраивая цепочку неравенств. Правда для 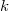 близких к
близких к 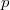 нужен будет специальный подход.
нужен будет специальный подход.
Есть кстати ещё гипотеза, что может неравенство и неверно.
Вычислительно получается при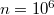 и
и 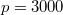 , что в конце 20 отрицательных значений (доходит до
, что в конце 20 отрицательных значений (доходит до 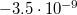 ).
).
Может это просто вычислительная ошибка, а может и само значение отрицательное.
Стоило бы присмотрется аналитически к случаю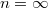 ,
, 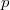 большое,
большое, 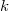 близко к
близко к 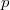 .
.
Есть и другие гармоники (в основном нечётные), но с меньшим весом.
Эта аппроксимация в целом положительная. Только в конце немного заходит в минус.
Наверно неравенство при
Есть кстати ещё гипотеза, что может неравенство и неверно.
Вычислительно получается при
Может это просто вычислительная ошибка, а может и само значение отрицательное.
Стоило бы присмотрется аналитически к случаю
Последний раз редактировалось zykov 01 май 2020, 19:47, всего редактировалось 1 раз.
Определитель вроде Вандермонда
Там видимо дело в том, что при больших  или при больших
или при больших 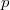 матрица приближается к сингулярной. Отсюда видимо вычислительные ошибки.
матрица приближается к сингулярной. Отсюда видимо вычислительные ошибки.
Так что случай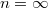 не подходит. Там матрица вырожденная.
не подходит. Там матрица вырожденная.
Например при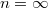 и
и 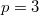 будет
будет 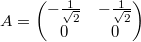 .
.
Так что случай
Например при
Определитель вроде Вандермонда
По поводу исходного вопроса про определитель матрицы, то у мена такой реультат.
Сначала (как я уже писал) делаем переходим к новой переменной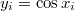 , тогда
, тогда 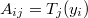 .
.
Где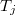 - полиномы Чебышева первого рода.
- полиномы Чебышева первого рода.
Если в матрице к одному столбцу добавить другой столбец (с любым множителем), то определитель матрицы не изменится. Таким образом в столбцах можно занулить все слагаемые, кроме самого старшего порядка и нулевого порядка. Например если к столбцу с кубическими многочленами добавить столбец с линейными многочленами умноженный на 3, то там останется только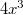 . А если к столбцу с многочленами 4-ой степени добавить столбец с квадратными многочленами умноженный на 4, то там останется только
. А если к столбцу с многочленами 4-ой степени добавить столбец с квадратными многочленами умноженный на 4, то там останется только 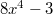 . Вобщем для нечётных остается только старшее слагаемое, для чётных будет два слагаемых - старшее и нулевой порядок.
. Вобщем для нечётных остается только старшее слагаемое, для чётных будет два слагаемых - старшее и нулевой порядок.
Т.е. будет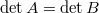 , где будет матрица
, где будет матрица 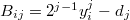 .
.
Для нечётных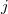 будет
будет 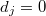 .
.
Для чётных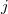 можно определить
можно определить 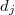 рекурсивно через предыдущие
рекурсивно через предыдущие 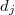 и коэффициенты полиномов Чебышева.
и коэффициенты полиномов Чебышева.
Для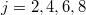 будет
будет 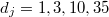 .
.
Для коэффициентов полиномов Чебышева есть прямая формула через факториалы.
Таким образом для чётных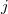 можно тоже получить прямую формулу
можно тоже получить прямую формулу 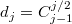 в виде биномиального коэффициента.
в виде биномиального коэффициента.
Если какой-то столбец в матрице разлагается на сумму (у нас это сумма старшего слагаемого и нулевого порядка), то определитель матрицы равен сумме определителей для матрицы с первым слагаемым и со вторым слагаемым. Т.е.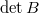 можно предстваить как сумму определителей нескольких матриц, где в каждом столбце только одно слагаемое. Если количество столбцов с чётными многочленами было
можно предстваить как сумму определителей нескольких матриц, где в каждом столбце только одно слагаемое. Если количество столбцов с чётными многочленами было 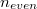 , то количество матриц будет
, то количество матриц будет 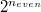 . Но если матрица содержит более одного столбца нулевого порядка, то её определитель просто равен нулю. Значит останется одно слагаемое, где нет столбцов нулевого порядка, и
. Но если матрица содержит более одного столбца нулевого порядка, то её определитель просто равен нулю. Значит останется одно слагаемое, где нет столбцов нулевого порядка, и 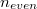 слагаемых, где на месте одного из столбцов с чётным многочленом стоит столбец нулевого порядка.
слагаемых, где на месте одного из столбцов с чётным многочленом стоит столбец нулевого порядка.
Обозначим как определитель Вандермонда
определитель Вандермонда 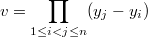 .
.
Обозначим единичные симметричные однородные многочлены порядка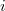 от
от 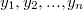 как
как 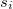 .
.
Например
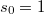
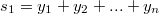
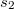 равен сумме произведений всех возможных выборок размера
равен сумме произведений всех возможных выборок размера 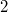 из
из  . Например при
. Например при 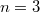 будет
будет 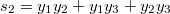 .
.
И так далее. В конце будет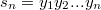 .
.
Ещё обозначим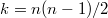 , так что произведение старших коэффициентов первых
, так что произведение старших коэффициентов первых  многочленов Чебышева равно
многочленов Чебышева равно 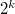 .
.
Первая матрица (которая без столбцов нулевого порядка) - это почти матрица Вандермонда, только начинается с первого порядка, а не с нулевого. И ещё столбцы имеют множители равные старшим коэффициентам многочленов Чебышева. Все эти коэффициенты можно вынести из определителя - получится множитель равный произведению этих коэффициентов. Так же из каждой строки можно вынести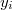 . Тогда останется только матрица Вандермонда (начинающаяся с нулевого порядка).
. Тогда останется только матрица Вандермонда (начинающаяся с нулевого порядка).
Таким образом определитель первой матрицы равен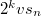 .
.
Остальные матрицы такие же, как и первая, только для чётного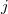 вместо столбца порядка
вместо столбца порядка 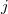 будет столбец нулевого порядка не со старшим коэффициентом полинома Чебышева, а с коэффициентом
будет столбец нулевого порядка не со старшим коэффициентом полинома Чебышева, а с коэффициентом 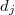 .
.
Если все коэффициенты вынести из определителя, то получится множитель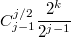 .
.
Если оставшийся единичный столбец нулевого порядка переставить в начало, то получится почти матрица Вандермонда. Она начинается с нулевого порядка, но порядок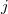 пропущен. Вместо него идёт порядок
пропущен. Вместо него идёт порядок 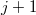 и далее порядки идут по очереди до
и далее порядки идут по очереди до  .
.
Определитель этой матрицы равен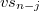 .
.
Отсюда кстати видно, что определитель первой матрицы соответствовал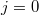 , что логично, так как там как раз был пропущен столбец нулевого порядка.
, что логично, так как там как раз был пропущен столбец нулевого порядка.
Вобщем в итоге ответ такой:
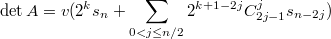
Сначала (как я уже писал) делаем переходим к новой переменной
Где
Если в матрице к одному столбцу добавить другой столбец (с любым множителем), то определитель матрицы не изменится. Таким образом в столбцах можно занулить все слагаемые, кроме самого старшего порядка и нулевого порядка. Например если к столбцу с кубическими многочленами добавить столбец с линейными многочленами умноженный на 3, то там останется только
Т.е. будет
Для нечётных
Для чётных
Для
Для коэффициентов полиномов Чебышева есть прямая формула через факториалы.
Таким образом для чётных
Если какой-то столбец в матрице разлагается на сумму (у нас это сумма старшего слагаемого и нулевого порядка), то определитель матрицы равен сумме определителей для матрицы с первым слагаемым и со вторым слагаемым. Т.е.
Обозначим как
Обозначим единичные симметричные однородные многочлены порядка
Например
И так далее. В конце будет
Ещё обозначим
Первая матрица (которая без столбцов нулевого порядка) - это почти матрица Вандермонда, только начинается с первого порядка, а не с нулевого. И ещё столбцы имеют множители равные старшим коэффициентам многочленов Чебышева. Все эти коэффициенты можно вынести из определителя - получится множитель равный произведению этих коэффициентов. Так же из каждой строки можно вынести
Таким образом определитель первой матрицы равен
Остальные матрицы такие же, как и первая, только для чётного
Если все коэффициенты вынести из определителя, то получится множитель
Если оставшийся единичный столбец нулевого порядка переставить в начало, то получится почти матрица Вандермонда. Она начинается с нулевого порядка, но порядок
Определитель этой матрицы равен
Отсюда кстати видно, что определитель первой матрицы соответствовал
Вобщем в итоге ответ такой:
Последний раз редактировалось zykov 07 май 2020, 17:14, всего редактировалось 1 раз.
Определитель вроде Вандермонда
Например
при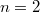 будет
будет 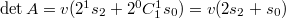
при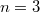 будет
будет 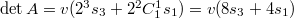
при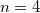 будет
будет 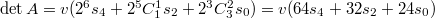
при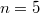 будет
будет 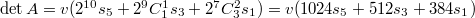
при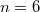 будет
будет 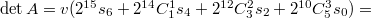
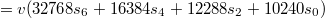
и т.д.
при
при
при
при
при
и т.д.
Последний раз редактировалось zykov 07 май 2020, 20:32, всего редактировалось 1 раз.
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей