Оценка нормы решения ДУ

Ian · Сообщение **Ian** » 05 апр 2020, 13:27

Рассматривается уравнение

x'(t)+\lambda x(t)=g(t),\;x(0)=0, где

g(t)>0 ограниченная, но не обязательно непрерывная (в этом смысле уравнение выполняется почти всюду)

\lambda >0 и если захотим, можем рассматривать только достаточно большие

\lambda .
Норма как для g, так и для x

||g||=ess \sup_{t\in [0,T]}|g(t)| -в смысле допускается

g(t)\leq ||g|| почти всюду, а не всюду.
Тогда наглядно очевидна оценка

||x||\leq\frac 1{\lambda}||g||, но не получается доказать
Есть даже формула для решения, но она не помогла

zykov · Сообщение **zykov** » 05 апр 2020, 21:53

Вроде решение будет: $x(t) = e^{-\lambda t} \int_0^t g(\tau) e^{\lambda \tau} \; d\tau$ .
Значит $|x(t)| \leq e^{-\lambda t} ||g|| \int_0^t e^{\lambda \tau} \; d\tau = ||g||\frac{1-e^{-\lambda t}}{\lambda} \leq ||g||\frac{1-e^{-\lambda T}}{\lambda} \leq \frac{||g||}{\lambda}$ .
Или я что-то упускаю?

При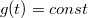 $g(t)=const$

достигается экстремум $\frac{1-e^{-\lambda T}}{\lambda}$ .

Ian · Сообщение **Ian** » 06 апр 2020, 03:36

Да, спасибо, сошлось. Первое рассуждение было таким. Пусть g- непрерывна, тогда либо в точке максимума |x(t)| x'=0, либо производная всюду больше 0, тогда максимум равен

x(T)<\frac 1{\lambda}g(T). А Вы показали, что первый случай тоже невероятен, даже для g=const>0

Портал Естественных Наук, версия 1.1