Открытая международная интернет-олимпиада
Известно, что
[math]-целое число, найти его.
Ответ-то я знаю, но как его по человечески искать без альфы
Вот еще одна с тем же свойством
[math]
OIIO-2020,2тур
OIIO-2020,2тур
Ian писал(а):Source of the post 22020∏2019k=1sinπk2020-целое число, найти его.
Ответ-то я знаю, но как его по человечески искать без альфы
Совсем в одну строчку у меня не получается.
Но так не сложно выходит используя школьную тригонометрию (
Последнее следует из двух формул, которые несложно доказать по индукции:
(1):
(2):
Первая при
Вторая при
Для индукции уже будет 4 случая: для каждой из двух по два случая - чётный или нечётный
Для первой формулы, если
Для первой формулы, если
И аналогично два случая для второй формулы.
Последний раз редактировалось zykov 29 мар 2020, 08:59, всего редактировалось 1 раз.
OIIO-2020,2тур
Спасибо, ну да ответ 2n=4040
OIIO-2020,2тур
Есть идея.
Судя по численным оценкам скорее всего
(
Тогда должно быть что
OIIO-2020,2тур
А если так
[math]
[math]
[math]
[math]
а должен получиться точный ряд для логарифма, степенной ряд же единственный
[math]
[math]
[math]
[math]
а должен получиться точный ряд для логарифма, степенной ряд же единственный
Последний раз редактировалось Ian 29 мар 2020, 09:05, всего редактировалось 1 раз.
OIIO-2020,2тур
Да, так тоже вроде сходится.
Для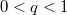 должно быть
должно быть 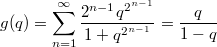 .
.
Разложение в ряд Тэйлора для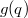 будет
будет 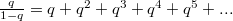 (сумма геометрической прогрессии).
(сумма геометрической прогрессии).
Для множителя внутри суммы можно тот же ряд записать: .
.
Получается:

Попробовал в Maxima конечную сумму посмотреть, получается например так:



Т.е. до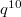 сошлось.
сошлось.
Вот до 20:
до 20:
Соответствует до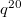 .
.
Для
Разложение в ряд Тэйлора для
Для множителя внутри суммы можно тот же ряд записать:
Получается:
Попробовал в Maxima конечную сумму посмотреть, получается например так:
Т.е. до
Вот
Соответствует до
OIIO-2020,2тур
Вот здесь

если подсобрать коэффициенты при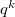 , то должна 1 получится.
, то должна 1 получится.
Для каждого конечного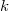 это будет конечное количество слагаемых.
это будет конечное количество слагаемых.
Например для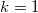 только
только 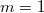 даёт
даёт 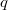 .
.
Для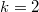 получается что
получается что 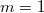 даёт
даёт 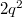 ,
, 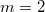 даёт
даёт 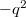 .
.
Для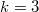 только
только 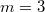 даёт
даёт 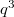 .
.
Для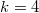 получается что
получается что 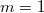 даёт
даёт 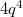 ,
, 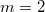 даёт
даёт 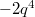 ,
, 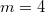 даёт
даёт 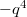 .
.
если подсобрать коэффициенты при
Для каждого конечного
Например для
Для
Для
Для
OIIO-2020,2тур
Проще говоря, любое k представляется в виде [math] с натуральными m,n конечным числом N способов, зависящих от степени двойки, на которую делится k. В них n меняется от 1 до этого N . но только при n=N будет m нечетное, и знак [math] положительный.Тогда собранный коэффициент при [math] будет
[math], где не исключается и тот случай, когда N=1
Значит, после приведения подобных получится ряд
[math]
Вот эта действительно олимпийская
PS. Ряд, заданный в условии, осуществляет ускорение сходимости такой прогрессии до гиперпрогрессии , первые 4 слагаемых уже дают 6 точных знаков. Что, конечно, практического значения не имеет, раз есть формула для суммы.
[math], где не исключается и тот случай, когда N=1
Значит, после приведения подобных получится ряд
[math]
Вот эта действительно олимпийская
PS. Ряд, заданный в условии, осуществляет ускорение сходимости такой прогрессии до гиперпрогрессии , первые 4 слагаемых уже дают 6 точных знаков. Что, конечно, практического значения не имеет, раз есть формула для суммы.
Последний раз редактировалось Ian 29 мар 2020, 14:30, всего редактировалось 1 раз.
OIIO-2020,2тур
Да, как-то так получается.
Если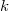 нечётное, то есть только одно слагаемое с коэффициентом "+1" (
нечётное, то есть только одно слагаемое с коэффициентом "+1" (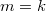 ).
).
Если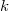 делится на 2, но не на 4, то есть два слагаемых - одно с "-1" (
делится на 2, но не на 4, то есть два слагаемых - одно с "-1" (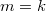 ) и одно с "+2" (
) и одно с "+2" (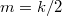 ).
).
Если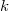 делится на 4, но не на 8, то есть три слагаемых - одно с "-1" (
делится на 4, но не на 8, то есть три слагаемых - одно с "-1" (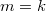 ), одно с "-2" (
), одно с "-2" (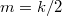 ) и одно с "+4" (
) и одно с "+4" (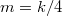 ).
).
И т.д. (чётные с "-", нечётные с "+").
с "-", нечётные с "+").
Если
Если
Если
И т.д. (чётные
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей