2. При каких целых n функция
[math]
имеет период [math] ?
Видимо, речь идет о минимальном положительном периоде. И тогда почему бы не спросить про нецелые n? Кажется, ничего не изменится
Олимпиада Росатом
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Олимпиада Росатом
Не очень понимаю, что олимпиадного в задаче, которая решается стандартной формулой суммы синусов. Про минимальный период как-то не подумал. Я правильно понимаю, что тогда ответ n=-34, -6, 8, 36?
А как вы предлагаете решать при произвольном n? Первое, что приходит в голову: разложить на два косинуса и искать случаи кратных периодов...
А как вы предлагаете решать при произвольном n? Первое, что приходит в голову: разложить на два косинуса и искать случаи кратных периодов...
Олимпиада Росатом
я не все эти значения нашел, может, ошибся.peregoudov писал(а): Я правильно понимаю, что тогда ответ n=-34, -6, 8, 36?
Есть такая олимпиадная идея -разложим [math], если она имеет период Т, то и 2-я производная будет иметь период Т [math] откуда нетрудно вывести что при [math] будут иметь период Т отдельно и [math], и [math]. Этим- пользоваться можете. Но пожалуйста построже
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Олимпиада Росатом
А просто подставить в функцию, не? Если отказаться от требования минимальности периода, есть еще два решения n=-4, 6, там период равен простоIan писал(а):Source of the post я не все эти значения нашел, может, ошибся.
Ну так я это и предложил. Получаем: периоды косинусовIan писал(а):Source of the post будут иметь период Т отдельно и cos ax, и cos bx. Этим- пользоваться можете.
Найденные выше целочисленные решения соответствуют (k,m)=(-235,-234), (-41,-36), (62,57), (256,255). Наверное, то, что в крайних парах числа отличаются на единицу, и свидетельствует о том, что за пределами интервала решений нет (там гипербола еще ближе к прямой k=m). Для n=-4,6 пары такие (k,m)=(-28,-21), (49,42).
Построже я не умею. Я могу мясо пожарить, а уж посолить-поперчить потом эпсилон-дельтой --- это вы сами.Ian писал(а):Source of the post Но пожалуйста построже
Для чего ограничили n целыми? Да решение существенно проще.
Ну да, правильному периоду соответствуют несократимые на общий множитель пары. А если можно сократить, то и период сокращается.
Олимпиада Росатом
peregoudov писал(а):после исключенияполучаем диофантово уравнение
. В непрерывных переменных это гипербола.
Найденные выше целочисленные решения соответствуют (k,m)=(-235,-234), (-41,-36), (62,57), (256,255). Наверное, то, что в крайних парах числа отличаются на единицу, и свидетельствует о том, что за пределами интервала решений нет (там гипербола еще ближе к прямой k=m). Для n=-4,6 пары такие (k,m)=(-28,-21), (49,42).
То есть Вы подбор не полностью проводили?
А классическое продолжение такое
[math]
Для проведения перебора заметим, что (k-m) и (k+m-21) разной четности, и два сомножителя, на которые будет разбита правая часть, разной четности. Значит, при всех вариантах приравнивания (k-m) и (k+m-21) этим сомножителям(они оба положительных или оба отрицательные) получится какая-то новая целочисленная пара (k,m)
Ну а из них надо полагать -новое n. То что n ищется целое -пока нигде не было использовано. Значит можно и нецелые найти
Ps. Вот такой список n нашелся
24 способа разбиения- 24 числа.
Но в некоторых вариантах [math] не будет наименьшим периодом, проверять надо
Код: Выбрать все
36
8
6
2
1,714285714
1,142857143
18,5
4,5
3,5
1,5
1,357142857
1,071428571
-34
-6
-4
0
0,285714286
0,857142857
-16,5
-2,5
-1,5
0,5
0,642857143
0,928571429
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Олимпиада Росатом
Я вообще диофантово уравнение не решал. Не люблю я этой возни с целыми числами... А проверка на период вроде бы очень простая: если k/m --- сократимая дробь, то и период меньшеIan писал(а):Source of the post То есть Вы подбор не полностью проводили?
Олимпиада Росатом
Пары у меня остались выписаны, и с ними много чего
Отбрасывая по этому критерию, останется 4 целых 36,8,-6,-34
2 полуцелых n=-16,5 ; -2,5
4 со знаменателем 7 : 12/7 ;8/7 ;2/7 ;6/7
и одно n со знаменателем 14 n=9/14
да, ни одного иррационального, потому что при целых k,m через них выражается n рациональными операциями
Отбрасывая по этому критерию, останется 4 целых 36,8,-6,-34
2 полуцелых n=-16,5 ; -2,5
4 со знаменателем 7 : 12/7 ;8/7 ;2/7 ;6/7
и одно n со знаменателем 14 n=9/14
да, ни одного иррационального, потому что при целых k,m через них выражается n рациональными операциями
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Олимпиада Росатом
Вот что у меня получилось: (множители, на которые раскладывается 14*35=490), (кратности периодов), наибольший общий делитель кратностей, значение n.
Если ставить условие, что период 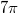 должен быть наименьшим, то выбираем строки с НОД=1. Вроде все сходится с вашими результатами.
должен быть наименьшим, то выбираем строки с НОД=1. Вроде все сходится с вашими результатами.
Код: Выбрать все
( 1, 490) ( 256, 255) 1 36
( -1,-490) (-235,-234) 1 -34
( 2, 245) ( 134, 132) 2 37/2
( -2,-245) (-113,-111) 1 -33/2
( 5, 98) ( 62, 57) 1 8
( -5, -98) ( -41, -36) 1 -6
( 10, 49) ( 40, 30) 10 9/2
( -10, -49) ( -19, -9) 1 -5/2
( 7, 70) ( 49, 42) 7 6
( -7, -70) ( -28, -21) 7 -4
( 14, 35) ( 35, 21) 7 7/2
( -14, -35) ( -14, 0) 14 -3/2
( 35, 14) ( 35, 0) 35 2
( -35, -14) ( -14, 21) 7 0
( 70, 7) ( 49, -21) 7 3/2
( -70, -7) ( -28, 42) 14 1/2
( 49, 10) ( 40, -9) 1 12/7
( -49, -10) ( -19, 30) 1 2/7
( 98, 5) ( 62, -36) 2 19/14
( -98, -5) ( -41, 57) 1 9/14
( 245, 2) ( 134,-111) 1 8/7
(-245, -2) (-113, 132) 1 6/7
( 490, 1) ( 256,-234) 2 15/14
(-490, -1) (-235, 255) 5 13/14Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость