Олимпиада ОММО для абитуриентов технических вузов
Мне непонятен даже подход к задаче 8
оммо-2020 задача 8
оммо-2020 задача 8
Для прямоугольного треугольника центр описанной около него окружности лежит в центре гипотенузы.
Значит центр описанной около этого тетраэдра сферы - это центр
Значит сумма сферических расстояний от любой точки до
Т.е. искомое множество - это множество точек для которых сумма сферических расстояний до
Для примера, если расположить плоскость экватора в плоскости
Вобщем, если из
Значит искомая площадь - это половина площади сферы, что равно
оммо-2020 задача 8
zykov писал(а):Source of the post это полупространство векторов имеющих острый угол с выбранным вектором
Может есть проще способ показать это, но вот первое что приходит на ум:
Вектора
Тогда
Значит
оммо-2020 задача 8
Обозначим [math] диаметрально противоположную точку на сфере
[math]
[math]
[math]
Значит из диаметрально противоположных точек, как правило, только одна принадлежит искомому множеству, а равенство это случай редкий(?)
[math]
[math]
[math]
Значит из диаметрально противоположных точек, как правило, только одна принадлежит искомому множеству, а равенство это случай редкий(?)
zykov писал(а):Значит искомая площадь - это половина площади сферы, что равно.
оммо-2020 задача 8
Ian писал(а):Source of the post Значит из диаметрально противоположных точек, как правило, только одна принадлежит искомому множеству
Да, это хороший аргумент. Остается доказать, что граница лежит в одной плоскости. Пока что это может быть любая центрально симметричная кривая на сфере.
Наверно получится дожать, если использовать диаметральные точки для
оммо-2020 задача 8
Для зеркальной симметрии будет:
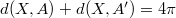 и
и 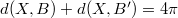 (то же самое для
(то же самое для 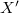 зеркально симметричной от
зеркально симметричной от 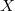 ).
).
И из зеркальной симметрии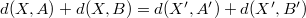 , т.к.
, т.к. 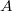 и
и 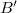 зеркально симметричны (и аналогично
зеркально симметричны (и аналогично 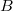 и
и  ).
).
Если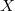 лежит на плоскости, то
лежит на плоскости, то 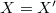 . Тогда
. Тогда 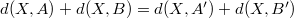 и
и 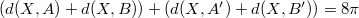 , т.е.
, т.е. 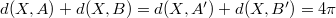 .
.
Если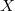 не лежит на плоскости, то
не лежит на плоскости, то 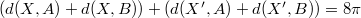 , т.е. одна сумма меньше
, т.е. одна сумма меньше 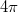 , другая больше.
, другая больше.
И из зеркальной симметрии
Если
Если
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость