Добрый день!
Подскажите, пожалуйста, есть ли какой-нибудь критерий, по которому можно определить возможность построения многогранника, а именно тетраэдра, с заданными длинами ребер?
Заранее спасибо.
Построение многогранника по заданным ребрам.
Построение многогранника по заданным ребрам.
Никогда про такой не слышал.
А положение рёбер на тетраэдре задано или вопрос в том, что какая-то комбинация будет допускать построение?
Просто у тетраэдра роль рёбер не одинаковая по отношению друг к другу. Для какого-то выбранного ребра четыре ребра будут примыкать к нему, а ещё одно будет ему противоположенно.
Если положение заданных рёбер фиксированно на тетраэдре, то для двух граней нужно проверить неравенство треугольника. А для последнего шестого ребра можно получить два неравенства (снизу и сверху) вращая плоскость одного из треугольников вокруг общего ребра со вторым. Экстремумы будут, когда плоскость этого треугольника совпадает с плоскостью второго треугольника (с одной или с другой строноны).
Если можно выбрать любое расположение данных рёбер на тетраэдре, то наверно нужно перебрать все комбинации. Так какое-то ребро можно выбрать первым (не важно какое). Для него можно выбрать одно из оставшихся в качестве противоположенного ребра - 5 вариантов. Оставшиеся четыре нужно разбить на две пары (без учёта порядка) - 3 варианта. И ещё 2 варианта - в этих парах какое ребро из второй пары будет противоположенно ребру из первой пары. Всего вроде 30 вариантов.
А положение рёбер на тетраэдре задано или вопрос в том, что какая-то комбинация будет допускать построение?
Просто у тетраэдра роль рёбер не одинаковая по отношению друг к другу. Для какого-то выбранного ребра четыре ребра будут примыкать к нему, а ещё одно будет ему противоположенно.
Если положение заданных рёбер фиксированно на тетраэдре, то для двух граней нужно проверить неравенство треугольника. А для последнего шестого ребра можно получить два неравенства (снизу и сверху) вращая плоскость одного из треугольников вокруг общего ребра со вторым. Экстремумы будут, когда плоскость этого треугольника совпадает с плоскостью второго треугольника (с одной или с другой строноны).
Если можно выбрать любое расположение данных рёбер на тетраэдре, то наверно нужно перебрать все комбинации. Так какое-то ребро можно выбрать первым (не важно какое). Для него можно выбрать одно из оставшихся в качестве противоположенного ребра - 5 вариантов. Оставшиеся четыре нужно разбить на две пары (без учёта порядка) - 3 варианта. И ещё 2 варианта - в этих парах какое ребро из второй пары будет противоположенно ребру из первой пары. Всего вроде 30 вариантов.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Построение многогранника по заданным ребрам.
Свой вариант предложу. Сначала для фиксированного соединения ребер. Очевидно, необходимым является неравенство треугольника для каких-то трех граней. Нетрудно видеть, что, если прибавить к нему условие, что сумма углов этих граней в общей вершине меньше 360 градусов, то получится необходимое и достаточное условие.
Если соединение ребер не фиксировано, то есть 6! перестановок ребер по тетраэдру, но это число нужно факторизовать по группе симметрии самого тетраэдра, которая совпадает с перестановкой вершин и содержит 4! элементов. Итого 30 комбинаций, как уже подсчитал zykov. Можно ли сократить число условий в этом случае, нужно еще подумать.
Если соединение ребер не фиксировано, то есть 6! перестановок ребер по тетраэдру, но это число нужно факторизовать по группе симметрии самого тетраэдра, которая совпадает с перестановкой вершин и содержит 4! элементов. Итого 30 комбинаций, как уже подсчитал zykov. Можно ли сократить число условий в этом случае, нужно еще подумать.
Построение многогранника по заданным ребрам.
Если есть 6 спичек, отношение наибольшей к наименьшей меньше [math], то из них всегда можно сложить тетраэдр. Если нет, то уже не обязательно)
Построение многогранника по заданным ребрам.
Ian писал(а):Source of the post Если нет, то уже не обязательно)
Т.е. либо можно, либо нет?
Построение многогранника по заданным ребрам.
Ian писал(а):Source of the post Если есть 6 спичек, отношение наибольшей к наименьшей меньше...
Вообще это отношение может быть сколь угодно большим. Берем правильный тетраэдр, ставим его на основание и вытягиваем верхнюю вершину вверх. Нижние ребра так и останутся неизменными, а боковые станут сколь угодно большими.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Построение многогранника по заданным ребрам.
Я тут немного поэксплуатировал железного друга, пытаясь понять, как будет выглядеть последнее условие zykov'а, если его расписать через длины ребер. Я начал с ребра  , к которому присоединил сначала ребра
, к которому присоединил сначала ребра  и
и  для образования треугольника, а затем --- ребра
для образования треугольника, а затем --- ребра 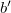 и
и 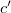 для образования второго треугольника (понятно, что
для образования второго треугольника (понятно, что 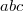 и
и 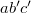 должны удовлетворять неравенству треугольника). Затем нашел минимальное
должны удовлетворять неравенству треугольника). Затем нашел минимальное 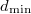 и максимальное
и максимальное  расстояния между вершинами, в которых сходятся
расстояния между вершинами, в которых сходятся 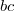 и
и 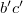 . Эти формулы достаточно просты и напоминают корни квадратного уравнения. Поэтому далее я написал неравенства для оставшейся стороны
. Эти формулы достаточно просты и напоминают корни квадратного уравнения. Поэтому далее я написал неравенства для оставшейся стороны 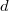 в виде
в виде 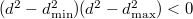 . В результате слева, после домножения на
. В результате слева, после домножения на 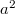 , получился однородный многочлен шестой степени
, получился однородный многочлен шестой степени


Хочется думать, что он инвариантен относительно группы симметрии тетраэдра (то есть перестановок ,
,  , ...
, ... 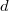 , соответствующих вращению и отражению тетраэдра, переводящих его в себя). Но это я пока не проверил, потому что пока не реализовал группу симметрии (насколько понимаю, достаточно реализовать отражение и два вращения вокруг разных осей). Хочется также думать, что сама структура этого выражения может быть как-то получена из групповых соображений.
, соответствующих вращению и отражению тетраэдра, переводящих его в себя). Но это я пока не проверил, потому что пока не реализовал группу симметрии (насколько понимаю, достаточно реализовать отражение и два вращения вокруг разных осей). Хочется также думать, что сама структура этого выражения может быть как-то получена из групповых соображений.
Хочется думать, что он инвариантен относительно группы симметрии тетраэдра (то есть перестановок

Построение многогранника по заданным ребрам.
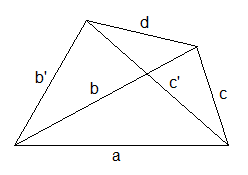
Эту сумму можно разбить на три слагаемых 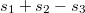 .
.
Слагаемое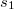 содержит три слагаемых для трёх пар противоположенных рёбер (например
содержит три слагаемых для трёх пар противоположенных рёбер (например  ).
).
Слагаемое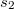 содержит четыре слагаемых для каждой грани (например
содержит четыре слагаемых для каждой грани (например  ).
).
Слагаемое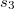 содержит двенадцать слагаемых для каждой цепочки из трёх рёбер не образующей треугольник (например
содержит двенадцать слагаемых для каждой цепочки из трёх рёбер не образующей треугольник (например  ). Таких вариантов 12, т.к. если взять какую-то вершину, то будет 6 цепочек в ней начинающихся (3 ребра из неё, дальше по 2 варианта) и 6 цепочек через неё проходящих ( 3 пары рёбер из неё, дальше по 2 варианта). Каждая такая цепочка захватывает все четыре вершины.
). Таких вариантов 12, т.к. если взять какую-то вершину, то будет 6 цепочек в ней начинающихся (3 ребра из неё, дальше по 2 варианта) и 6 цепочек через неё проходящих ( 3 пары рёбер из неё, дальше по 2 варианта). Каждая такая цепочка захватывает все четыре вершины.
Каждое из этих слагаемых симметрично относительно перестановки рёбер сохраняющей свойство "быть противоположенными для двух рёбер".
Слагаемое
Слагаемое
Слагаемое
Каждое из этих слагаемых симметрично относительно перестановки рёбер сохраняющей свойство "быть противоположенными для двух рёбер".
Построение многогранника по заданным ребрам.
Ещё  можно переписать как сумму по всем тройкам рёбер (3 из 6 будет 20) произведений квадратов их длин, но с коэффициентом:
можно переписать как сумму по всем тройкам рёбер (3 из 6 будет 20) произведений квадратов их длин, но с коэффициентом: 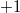 - если это треугольник (4 случая, 0 концов),
- если это треугольник (4 случая, 0 концов), 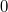 - если это три ребра из одной вершины (4 случая, 3 конца),
- если это три ребра из одной вершины (4 случая, 3 конца), 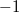 - если это цепочка из трёх рёбер (12 случаев, 2 конца).
- если это цепочка из трёх рёбер (12 случаев, 2 конца).
Построение многогранника по заданным ребрам.
При длинах спичек [math] и 5 спичек по 1 сложить нельзяzykov писал(а):Ian писал(а):Source of the post Если нет, то уже не обязательно)
Т.е. либо можно, либо нет?
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Построение многогранника по заданным ребрам.
Да, я тоже заметил. Это как раз классы, инвариантные относительно преобразований симметрии тетраэдра, что подтверждает мое подозрение, что левая часть неравенства инвариантна.zykov писал(а):Source of the post Слагаемоесодержит три слагаемых для трёх пар противоположенных рёбер (например
).
Слагаемоесодержит четыре слагаемых для каждой грани (например
).
Слагаемоесодержит двенадцать слагаемых для каждой цепочки из трёх рёбер не образующей треугольник
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость