Опять МФТИ
Опять МФТИ
3-6 курс.4.
Предположим, в единичном шаре некоторого евклидова пространства находится [math] точек [math]. Докажите, что их можно разбить на два множества по [math] точек каждое таким образом, что центры масс этих множеств окажутся на расстоянии не более [math] друг от друга
Соображения по решению.
Для [math] точек можно найти [math]-мерную гиперплоскость, содержащую все точки, в сечении гиперплоскостью любого единичного шара получится шар радиуса не больше 1, поэтому можем далее считать, что размерность пространства равна [math].
Например [math], для тетраэдра , вписанного в единичный шар, минимальное расстояние между серединами противоположных ребер у правильного тетраэдра,[math]-требуемая оценка не для всех [math] является точной
Пусть перемещением одной точки мы хотим максимально испортить возможность сделать центры тяжести близко. Тогда возьмем гиперплоскость, содержащую остальные точки, и перпендикулярную ей ось через их центр тяжести. [math]-ю точку отодвинем на этой оси так далеко от гиперплоскости, как позволяет объемлющий шар, на некоторое расстояние [math] Тогда мы точно можем сказать, что проекции центров тяжести на эту ось находятся на [math] друг от друга, ведь одно множество содержит двинутую точку, другое нет.
А что изменяется - при оптимальном движении и гиперплоскость должна немного отодвинуться от центра шара и в сечении дать шар чуть меньшего диаметра (как плоскость основания вписанного правильного тетраэдра отодвинута от центра вниз, а вершина вверх до упора в шар). Попробовать отодвинуть 2 точки, каждую по своей новой координате, и будет какая-то рекуррентность по [math] для конструкций . И сделать из этого рекуррентность для оценок
Предположим, в единичном шаре некоторого евклидова пространства находится [math] точек [math]. Докажите, что их можно разбить на два множества по [math] точек каждое таким образом, что центры масс этих множеств окажутся на расстоянии не более [math] друг от друга
Соображения по решению.
Для [math] точек можно найти [math]-мерную гиперплоскость, содержащую все точки, в сечении гиперплоскостью любого единичного шара получится шар радиуса не больше 1, поэтому можем далее считать, что размерность пространства равна [math].
Например [math], для тетраэдра , вписанного в единичный шар, минимальное расстояние между серединами противоположных ребер у правильного тетраэдра,[math]-требуемая оценка не для всех [math] является точной
Пусть перемещением одной точки мы хотим максимально испортить возможность сделать центры тяжести близко. Тогда возьмем гиперплоскость, содержащую остальные точки, и перпендикулярную ей ось через их центр тяжести. [math]-ю точку отодвинем на этой оси так далеко от гиперплоскости, как позволяет объемлющий шар, на некоторое расстояние [math] Тогда мы точно можем сказать, что проекции центров тяжести на эту ось находятся на [math] друг от друга, ведь одно множество содержит двинутую точку, другое нет.
А что изменяется - при оптимальном движении и гиперплоскость должна немного отодвинуться от центра шара и в сечении дать шар чуть меньшего диаметра (как плоскость основания вписанного правильного тетраэдра отодвинута от центра вниз, а вершина вверх до упора в шар). Попробовать отодвинуть 2 точки, каждую по своей новой координате, и будет какая-то рекуррентность по [math] для конструкций . И сделать из этого рекуррентность для оценок
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Опять МФТИ
А размерность евклидова пространства какая? Может быть, тут надо какие-то неравенства для первого и второго моментов употребить?
Опять МФТИ
судя по тексту, размерность как угодно велика. "Евклидово" -значит расстояние считается по теореме Пифагора.
Я показал, что размерность выше 2m-1 смотреть не стоит
Например, как частный случай может быть задача про 4 точки в шаре в двадцатимерном пространстве. Но тогда существует трехмерная гиперплоскость, содержащая все 4 точки, в пересечении с шаром она дает трехмерный шар радиуса не больше 1, и можно решать в нем.
Я показал, что размерность выше 2m-1 смотреть не стоит
Например, как частный случай может быть задача про 4 точки в шаре в двадцатимерном пространстве. Но тогда существует трехмерная гиперплоскость, содержащая все 4 точки, в пересечении с шаром она дает трехмерный шар радиуса не больше 1, и можно решать в нем.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Опять МФТИ
Да, я, как всегда, из вашей рваной речи не понял, о чем вы. Теперь понял с размерностью.
Меня в этой задаче смущает необходимость выбора. Нужно сформулировать какой-то критерий и доказать его. Причем просто добавлять точки не получится, потому что добавление новой пары может потребовать кардинально перестроить прежнее разбиение. Нужно начинать с того, что все точки уже даны. Была у меня еще идея вместо исходных точек рассматривать центры масс всех выборок m из 2m, но она пока ничего не дала...
Меня в этой задаче смущает необходимость выбора. Нужно сформулировать какой-то критерий и доказать его. Причем просто добавлять точки не получится, потому что добавление новой пары может потребовать кардинально перестроить прежнее разбиение. Нужно начинать с того, что все точки уже даны. Была у меня еще идея вместо исходных точек рассматривать центры масс всех выборок m из 2m, но она пока ничего не дала...
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Опять МФТИ
Собственно, похоже, что сработала еще одна идея: если не знаешь, как выбрать, попробуй доказать некую оценку для суммы всех вариантов, тогда из нее будет следовать оценка для по крайней мере одного из слагаемых.
Обозначим через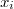 радуис-векторы отдельных точек, а через
радуис-векторы отдельных точек, а через 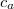 --- радиус векторы всевозможных центров масс выборок m из 2m точек. Через
--- радиус векторы всевозможных центров масс выборок m из 2m точек. Через 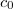 обозначим центр масс всех 2m точек, он же --- центр масс всех центров масс. Тогда, если я правильно сосчитал (считал долго и муторно, но мне кажется, это должно быть как-то очевидно из матстатистики)
обозначим центр масс всех 2m точек, он же --- центр масс всех центров масс. Тогда, если я правильно сосчитал (считал долго и муторно, но мне кажется, это должно быть как-то очевидно из матстатистики)
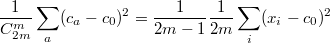
Сумму справа вроде бы можно мажорировать единицей, тогда по крайней мере для одной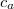 должно выполняться
должно выполняться
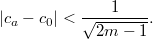
А расстояние между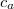 и центром масс остатка вдвое больше.
и центром масс остатка вдвое больше.
Обозначим через
Сумму справа вроде бы можно мажорировать единицей, тогда по крайней мере для одной
А расстояние между
Опять МФТИ
peregoudov писал(а): мне кажется, это должно быть как-то очевидно из матстатистики)
Есть такая формула в дисперсионном анализе -общая дисперсия равна сумме межгрупповой и средней внутригрупповой дисперсий. Это результат сложного раскрытия скобок в сумме квадратов.
Группы будем считать - всевозможные наборы m точек. Каждая точка получается повторена в ген.совокупности ровно [math] раз
Межгрупповая средняя совпадает с общей средней, поэтому межгрупповая дисперсия и общая дисперсия считаются от одного центра [math]. А внутригрупповые средние могут быть разные и куда их приткнуть
Опять МФТИ
Вроде похоже на правду. По крайней мере для тетраэдра совпадает с экстремумом
Это более строгая оценка, чем требовалось -
Наверно они имели ввиду какое-то другое, более простое, решение...
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Опять МФТИ
Я не понял, вы что-то имеете против моего решения?Ian писал(а):Source of the post А внутригрупповые средние могут быть разные и куда их приткнуть
Собственно, так и считалось. Давайте тогда напишу детали расчета, раз возникают вопросы.Ian писал(а):Source of the post Каждая точка получается повторена в ген.совокупности ровнораз
Но вообще из матстатистики результат довольно очевидный. Если у нас есть n измерений, а дисперсия каждого измерения
Мне кажется, идея была именно такая, как я написал выше. Просто не были уверены, какое число брать: размер выборки или размер полной совокупности.zykov писал(а):Source of the post Наверно они имели ввиду какое-то другое, более простое, решение...
Запишем среднее по выборке
Здесь
Если
Подставляя, получаем
Добавляем ко второй сумме диагональную часть и вычитаем такую же из первой
Первая сумма в результате дает
Опять МФТИ
Да, у меня так же вышло.
Последний шаг лишний.
Вот это -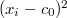 - уже нельзя мажорировать единицей (оно может быть и больше 1, но не больше 4).
- уже нельзя мажорировать единицей (оно может быть и больше 1, но не больше 4).
Достаточно так:
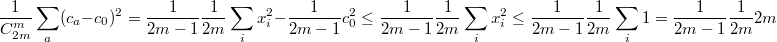
Если известно, что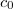 не равно нулю, то просто оценка будет ещё строже:
не равно нулю, то просто оценка будет ещё строже:
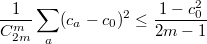
Последний шаг лишний.
Вот это -
Достаточно так:
Если известно, что
Последний раз редактировалось zykov 19 дек 2019, 18:32, всего редактировалось 1 раз.
Опять МФТИ
peregoudov, спасибо за содержательный пост
Вот еще одна
3-6 курс
5. Докажите неравенство[math] для любых действительных чисел [math], для которых [math]
Эту решил но сложным путем
Вот еще одна
3-6 курс
5. Докажите неравенство[math] для любых действительных чисел [math], для которых [math]
Эту решил но сложным путем
Последний раз редактировалось Ian 20 дек 2019, 03:59, всего редактировалось 1 раз.
Опять МФТИ
Ian писал(а):Source of the post Эту решил но сложным путем
Это как?
Переходим просто в другой базис - дискретное преобразование Фурье. Там оператор дискретной производной будет диагональным.
Опять МФТИ
Поправил в условии коэффициент.
И сразу шаг в сторону непрерывной задачи [math], почему мы с Вами 2 раза уже в предыдущих темах там Фурье не применили (доопределив функцию вне отрезка нулем)
Впрочем, в классе [math] из [math] есть решение еще проще - рассмотрим ее синус- коэффициенты Фурье, сразу видно , что у оптимальной функции только при [math] он отличен от нуля.
И сразу шаг в сторону непрерывной задачи [math], почему мы с Вами 2 раза уже в предыдущих темах там Фурье не применили (доопределив функцию вне отрезка нулем)
Впрочем, в классе [math] из [math] есть решение еще проще - рассмотрим ее синус- коэффициенты Фурье, сразу видно , что у оптимальной функции только при [math] он отличен от нуля.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Опять МФТИ
Ну да, я ж обычно бессодержательно пишу...Ian писал(а):Source of the post peregoudov, спасибо за содержательный пост
Ни фига не понял...zykov писал(а):Source of the post- это квадрат вектора
, который как известно не зависит от базиса.
- это квадрат вектора
(линейный оператор от
- дискретная производная), который так же не зависит от базиса.
Переходим просто в другой базис - дискретное преобразование Фурье. Там оператор дискретной производной будет диагональным.
Опять МФТИ
peregoudov писал(а):Source of the post Ни фига не понял...
Единственное что надо обиграть, это ограничение на подпространство (проекцию):
PS: Да, стандартный ход в DFT - это периодическое дополнение (
Опять МФТИ
В такой форме это можно сделать. "В лоб", как условный экстремум. Но получается несколько тяжеловесно. (Там 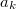 комплексные.)
комплексные.)
Если доопределить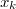 по-другому - сначала расширить его до интервала от
по-другому - сначала расширить его до интервала от 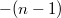 до
до  так чтобы было нечётное (
так чтобы было нечётное (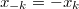 ).
).
А потом уже доопределить периодически от этого двойного интервала (период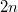 ) и брать Фурье, то в Фурье только синусы останутся без косинусов. Ограничение
) и брать Фурье, то в Фурье только синусы останутся без косинусов. Ограничение 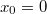 получается автоматом.
получается автоматом.
В разложении Фурье можно скомбинировать члены, как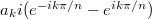 . Здесь уже
. Здесь уже 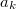 будут действительные.
будут действительные.
Константы уже не будет в разложении (у неё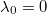 ). Минимальное
). Минимальное 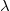 будет
будет 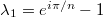 , которое и даст минимальную норму после действия оператора.
, которое и даст минимальную норму после действия оператора.
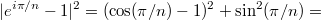
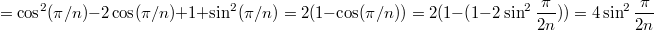
Экстремальные будут
будут 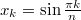 .
.
Если доопределить
А потом уже доопределить периодически от этого двойного интервала (период
В разложении Фурье можно скомбинировать члены, как
Константы уже не будет в разложении (у неё
Экстремальные
Опять МФТИ
Ian писал(а):Source of the post И сразу шаг в сторону непрерывной задачи, почему мы с Вами 2 раза уже в предыдущих темах там Фурье не применили (доопределив функцию вне отрезка нулем)
Да, здесь можно аналогично сделать.
Доопределить
Для периодической функции получим ряд Фурье. Т.к. она нечётная, то амплитуды косинусов будут нулевые (в том числе и амплитуда константы). Останутся только синусы.
Самые маленькие по абсолютной величине собственные значения войдут в
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Опять МФТИ
Ну, про циркулянты и Фурье я слыхал. Просто сначала не понял, что 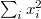 стоит множителем, а не под синусом. Так вы предлагаете трактовать это неравенство как оценку нормы квадратичной формы
стоит множителем, а не под синусом. Так вы предлагаете трактовать это неравенство как оценку нормы квадратичной формы 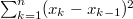 ? Ее матрица
? Ее матрица
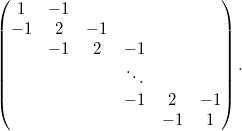
Раз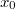 и
и 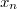 нулевые, матрицу можно обрезать
нулевые, матрицу можно обрезать
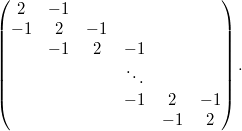
Это не циркулянт и преобразованием Фурье не диагонализуется.
Но мне кажется, что тут имелась в виду физика, одномерная цепочка масс, связанных пружинками. Решение для собственного вектора ищется в виде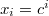 , для
, для  из каждой строки, кроме первой и последней, получается квадратное уравнение
из каждой строки, кроме первой и последней, получается квадратное уравнение 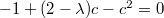 , так что общее решение
, так что общее решение 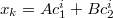 , из первой и последней строк тогда получаем
, из первой и последней строк тогда получаем
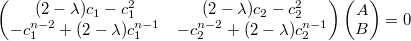
Немного замучено, но, если учесть, что по теореме Виета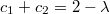 ,
, 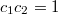 , то все упрощается до
, то все упрощается до
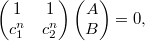
так что собственные значения определяются из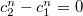 или
или 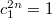 . Откуда и получаем
. Откуда и получаем 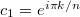 ,
, 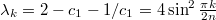 . Нулевое собственное значение исключено, посколку для него получаем
. Нулевое собственное значение исключено, посколку для него получаем 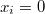 .
.
Раз
Это не циркулянт и преобразованием Фурье не диагонализуется.
Но мне кажется, что тут имелась в виду физика, одномерная цепочка масс, связанных пружинками. Решение для собственного вектора ищется в виде
Немного замучено, но, если учесть, что по теореме Виета
так что собственные значения определяются из
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Опять МФТИ
Мне кажется, тогда уж проще так:Ian писал(а):И сразу шаг в сторону непрерывной задачи [math], почему мы с Вами 2 раза уже в предыдущих темах там Фурье не применили (доопределив функцию вне отрезка нулем)
и получаем задачу на поиск минимума оператора энергии для частицы в яме с бесконечными стенками.
Опять МФТИ
peregoudov писал(а):Source of the post и получаем задачу на поиск минимума оператора энергии для частицы в яме с бесконечными стенками
И как этот минимум ищется?
Так же - через вариационное исчисление (универсальный метод) или, в данном случае, через спектр (Min-max theorem).
Опять МФТИ
peregoudov писал(а):Source of the post Так вы предлагаете трактовать это неравенство как оценку нормы квадратичной формы
Вовсе нет. Там же русским языком написано: дискретная производная - первая, а не вторая.
А квадрат - это уже для нахождения нормы этого вектора.
Вобщем на википедии всё написано:
zykov писал(а):Source of the post через спектр (Min-max theorem).
Замечание: там
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 17 гостей