Лед на пруду

[peregoudov]

Невообразимо плохо у нас идут физические задачки, даже уже и школьные Что ж, попытаюсь еще раз.

Температура воздуха, долгое время державшаяся на нуле, в ночь резко упала до -5 градусов и на пруду начал намерзать лед. По какому закону меняется толщина льда со временем?

[zykov]

Какого-то красивого решения не видно. А "в лоб" - составляем одномерную систему диффуров и решаем.

Пусть ось [math]X направлена вглубь льда, так что граница "лёд-воздух" находится при [math]x=0, граница "лёд-вода" находится при [math]x=x_0(t), [math]t - время, [math]T - температура.
Тогда имеем стандартное уравнение теплопроводности [math]C\frac{dT(x,t)}{dt}=k\frac{\partial^2 T(x,t)}{\partial x^2}.
[math]C - теплоёмкость льда, [math]k - теплопроводность льда.
Граничные условия: [math]T(0,t)=-5^\circ C, [math]T(x_0(t),t)=0^\circ C.

Второе уравнение получается из условия компенсации тепла замерзания потоком тепла теплопроводности: [math]\lambda\rho\frac{dx_0(t)}{dt}=k\frac{\partial T(x,t)}{\partial x}\mid_{x=x_0(t)}.
[math]\lambda - теплота плавления/замерзания льда, [math]\rho - плотность льда.


Возможно получится отказатся от первого уравнения в частных производных, если динамические эффекты в слое льда невелики и можно приближенно считать распределение температуры линейным, а поток тепла постоянным по всей толще. Это нужно в цифрах прикинуть.

[zykov]

Уточнение, тут [math]C - теплоёмкость на единицу объёма.
Обычно указывают [math]c - теплоёмкость на единицу массы. Так что [math]C=c\rho.
Уравнение теплопроводности нужно записать [math]c\rho\frac{\partial T(x,t)}{\partial t}=k\frac{\partial^2 T(x,t)}{\partial x^2}.

[zykov]

Можно сравнить, сколько тепла идёт на намерзание и на дополнительное охлаждение льда при намерзании, чтобы оценить точность приближения линейного распределения температуры.

Так на намерзание единицы глубины льда (единичной площади) уходит [math]\lambda\rho тепла (точнее холода).
На дополнительное охлаждение более толстого слоя льда уходит [math]0.5c\rho\Delta T холода.
Т.е. нужно сравнить [math]\lambda и [math]0.5c\Delta T.
Для льда [math]\lambda=335 ~ кДж/кг и [math]0.5c\Delta T=0.5*2.06~кДж/(кг*К)*5~К=5.15 ~ кДж/кг.

Первое получается значительно больше второго (почти на два порядка), так что можно использовать приближенную модель линейного распределения температуры и отказатся от диффура в частных производных.
Тогда остаётся одно обычное диф.уравнение [math]\lambda\rho\frac{dx_0(t)}{dt}=k\frac{\Delta T}{x_0(t)}.

Решаем: [math]\lambda\rho x_0dx_0=k\Delta T dt, ~~~~ 0.5\lambda\rho dx_0^2=k\Delta T dt, ~~~~ 0.5\lambda\rho x_0^2(t)=k\Delta T t.
Получаем [math]x_0(t)=\sqrt {\frac{2k\Delta T}{\lambda\rho}t}.

[peregoudov]

Да, так и есть.

[zykov]

Только более точно было бы в эту формулу подставить вместо [math]\lambda сумму [math]\lambda+0.5c\Delta T, чтобы учесть тепло на охлаждение льда (340 кДж/кг вместо 335 кДж/кг).

[peregoudov]

Только вот у меня еще получается, что зависимость 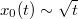точная, а не приближенная. Правда, получается это в результате довольно жесткого матана (под катом), но мне кажется, должен быть способ проще это увидеть.

Можно выбрать единицы измерения так, чтобы в уравнениях не осталось лишних множителей, а в граничные условия будет входить только температура воздуха







Теперь делаем финт ушами: переходим от переменных к переменным (при этом становится функцией ) по формуле . Задача переписывается в виде (индексы обозначают дифференцирование)







Ищем решение в виде . Для получаем задачу





Уравнение для может быть стандартным методом решено, общее решение



Граничные условия можно удовлетворить при любом , при этом



P. S. В общем, допер.
Дело тут в том, что решение, как видно из ответа, нужно было искать в скейлинговой форме . Тогда уравнение превращается в



(), а граничное условие намерзания --- в



поэтому, полагая , получим , оставшиеся граничные условия превращаются в и . Дальше снова все решается, ответ тот же, что под катом выше.