Да, вы, батенька, садист, сразу лагранжианом по башке

А вообще забавно, согласитесь, что вся энергия тут --- кинетическая, но при этом она не сохраняется, а сохраняется другая величина (кстати, а почему вы упорно не пользуетесь лагранжевыми законами сохранения, а напрямую решаете лагранжевы уравнения --- это ведь сложнее?) А не сохраняется она потому, что вращающийся цилиндр над натянутой нитью совершает работу. И вот это наблюдение дает возможность решить задачу почти школьным методом.
Разобьем скорость массы m на параллельную и перпендикулярную нити. Параллельная связана с вращением цилиндра
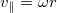
, а перпендикулярная определяет силу натяжения
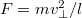
, а вслед за ней --- мощность, развиваемую вращающимся цилиндром
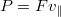
, которая равна производной кинетической энергии
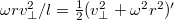
. Изменение длины нити связано как с вращением цилиндра (вклад
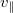
), так и с разматыванием нити за счет движения массы вокруг цилиндра (вклад
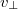
)
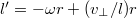
. В итоге имеем два уравнения
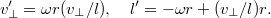
Из них находим
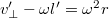
, откуда
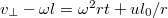
. Подставляя в уравнение для l, находим
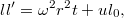
откуда уже
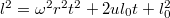
(ответ, естественно, тот же, что у вас). Нить не сможет полностью намотаться, если квадратный трехчлен в правой части имеет отрицательный дискриминант, а это происходит при
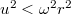
.
Но еще красивее решение с переходом во вращающуюся систему отсчета. Там скорость массы перпендикулярна нити, а работу совершает только центробежная сила, поэтому уравнения упрощаются до
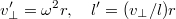
и интегрируются впрямую.
 вращается с постоянной угловой скоростью
вращается с постоянной угловой скоростью  . На него намотана невесомая нерастяжимая нить, на свободном конце нити укреплена точечная масса
. На него намотана невесомая нерастяжимая нить, на свободном конце нити укреплена точечная масса  . Длину свободного конца нити как функцию времени обозначим за
. Длину свободного конца нити как функцию времени обозначим за 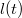 . Известны начальная длина свободного конца
. Известны начальная длина свободного конца 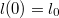 и скорость изменения длины в начальный момент
и скорость изменения длины в начальный момент 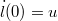 . Нить считаем всегда натянутой. Найти
. Нить считаем всегда натянутой. Найти 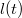 . Показать, что при определенных условиях (каких?) нить никогда не сможет полностью намотаться на цилиндр.
. Показать, что при определенных условиях (каких?) нить никогда не сможет полностью намотаться на цилиндр.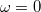 --- это намного проще.
--- это намного проще.