Израильский суперфинал
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Израильский суперфинал
Мне кажется, рассуждения можно упростить, если вместо 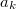 ввести их частичные суммы
ввести их частичные суммы  . Условия задачи тогда переписываются в виде
. Условия задачи тогда переписываются в виде  ,
, 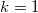 , ...
, ...  ,
, 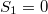 . И дальше, наверное, нужно какие-то соотношения по модулю n между индексами рассматривать. Если выписывать матрицу, то в ней, помимо главной диагонали из единиц, еще две "диагонали" вдвое меньшего наклона из -1. А можно еще рисовать графы.
. И дальше, наверное, нужно какие-то соотношения по модулю n между индексами рассматривать. Если выписывать матрицу, то в ней, помимо главной диагонали из единиц, еще две "диагонали" вдвое меньшего наклона из -1. А можно еще рисовать графы.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Израильский суперфинал
И нам надо изучить свойства отображения  .
.
Для нечетного это перестановка, потому что разные
это перестановка, потому что разные 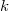 отображаются в разные
отображаются в разные 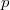 . Действительно
. Действительно 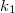 и
и 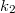 могут отобразиться в одно и то же
могут отобразиться в одно и то же 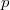 , только если
, только если  , что при нечетных
, что при нечетных  невозможно.
невозможно.
Всегда существует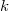 , отображающееся само в себя. Оно определяется уравнением
, отображающееся само в себя. Оно определяется уравнением 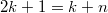 и равно
и равно 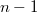 .
.
Из сказанного следует, что в перестановке при нечетных есть цикл единичной длины
есть цикл единичной длины 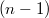 , соответствующую переменную можно взять ненулевой. Это воспроизводит уже полученное выше решение для нечетных
, соответствующую переменную можно взять ненулевой. Это воспроизводит уже полученное выше решение для нечетных  .
.
Если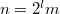 с нечетным
с нечетным  , то существует последовательность отображения индексов
, то существует последовательность отображения индексов

Последний индекс отображается сам в себя, а получить первый член отображением невозможно, так как нечетно, а
нечетно, а 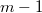 четно. Таким образом, существует отдельная ветвь графа, не содержащая индекса 1, соответствующие переменные можно взять ненулевыми. Это воспроизводит решение Ian'а для
четно. Таким образом, существует отдельная ветвь графа, не содержащая индекса 1, соответствующие переменные можно взять ненулевыми. Это воспроизводит решение Ian'а для  , содержащих нечетный множитель.
, содержащих нечетный множитель.
Наконец, для четных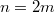 замечаем, что четные индексы отображаются в нечетные, а нечетные --- сами в себя, поэтому достаточно рассмотреть отображение только нечетных индексов, подставляя
замечаем, что четные индексы отображаются в нечетные, а нечетные --- сами в себя, поэтому достаточно рассмотреть отображение только нечетных индексов, подставляя 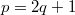 и
и 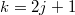 имеем
имеем  . Получили ту же задачу, только с вдвое меньшим
. Получили ту же задачу, только с вдвое меньшим  . Для
. Для 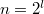 можно продолжить, сведя к
можно продолжить, сведя к 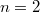 , для которого отсутствие нетривиальных решений проверяется непосредственно. Для
, для которого отсутствие нетривиальных решений проверяется непосредственно. Для 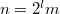 можно свести к нечетному
можно свести к нечетному  , для которого существование нетривиального решения уже доказана.
, для которого существование нетривиального решения уже доказана.
Для нечетного
Всегда существует
Из сказанного следует, что в перестановке при нечетных
Если
Последний индекс отображается сам в себя, а получить первый член отображением невозможно, так как
Наконец, для четных
Израильский суперфинал
Действительно, уравнения задают присваивания [math] друг другу (а [math] нулю) по орбитам отображения [math] и при [math] надо доказать, что в присваивания будут вовлечены все возможные остатки k=0,1...(n-1). Каждый индекс k запишем в двоичной системе [math]-значным числом(n и 0 отождествляем), отображение сдвигает знаки влево (с потерей самого левого знака) и приписывает единицу справа. Ясно что оно любую двоичную запись превратит не более чем за [math] шагов в (1...1)=n-1, значит, все [math] равны, значит, нулю.
Случай, когда n не степень двойки, уже имеет простое доказательство в лоб, примером расстановки
Случай, когда n не степень двойки, уже имеет простое доказательство в лоб, примером расстановки
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей