Интегрально-функциональное уравнение
Интегрально-функциональное уравнение
В МГУ на зачете предложили. Имеет ли уравнение [math]п.в. - ненулевые решения, принадлежащие [math]?
Мое мнение, что нет. Например, можно подобрать трансцедентное [math], что [math] всюду, кроме 0, удовлетворяет этому уравнению, но оказывается [math] и функция не принадлежит [math].
Но множество функций, удовлетворяющих этому уравнению, бесконечно. Зададим [math] на [math] произвольно, находим на на [math] функцию x(t) из условия:
[math] для всех [math], и так далее на промежутках [math], но функция должна еще склеиваться по непрерывности на границах промежутков, и это должно привести к росту модулей значений вблизи 0 со скоростью не меньше [math], и значит, к неинтегрируемости. Но не вижу, как доказать
Мое мнение, что нет. Например, можно подобрать трансцедентное [math], что [math] всюду, кроме 0, удовлетворяет этому уравнению, но оказывается [math] и функция не принадлежит [math].
Но множество функций, удовлетворяющих этому уравнению, бесконечно. Зададим [math] на [math] произвольно, находим на на [math] функцию x(t) из условия:
[math] для всех [math], и так далее на промежутках [math], но функция должна еще склеиваться по непрерывности на границах промежутков, и это должно привести к росту модулей значений вблизи 0 со скоростью не меньше [math], и значит, к неинтегрируемости. Но не вижу, как доказать
Интегрально-функциональное уравнение
Ian писал(а):Source of the post можно подобрать трансцедентное
(но при этом интеграл расходится)
Интегрально-функциональное уравнение
Ian писал(а):Source of the postдля всех,
Должно быть
Интегрально-функциональное уравнение
Как-то трудно двигается. [math]
[math] из уравнения непрерывна, обращается в 0 в нуле, и дифференцируема п.в.
[math].
Пусть [math] ,[math] функция на [math], обращающаяся в 0 на - бесконечности
Тогда она удовлетворяет дифференциально-разностному уравнению
[math], которое имеет, в соответствии с уже найденными альфами, пару линейно независимых решений [math] и [math], а какие еще, и есть ли среди них те, по которым получится [math]
При другом коэффициенте в уравнении могли бы получиться и осциллирующие решения, напр.[math]
[math] из уравнения непрерывна, обращается в 0 в нуле, и дифференцируема п.в.
[math].
Пусть [math] ,[math] функция на [math], обращающаяся в 0 на - бесконечности
Тогда она удовлетворяет дифференциально-разностному уравнению
[math], которое имеет, в соответствии с уже найденными альфами, пару линейно независимых решений [math] и [math], а какие еще, и есть ли среди них те, по которым получится [math]
При другом коэффициенте в уравнении могли бы получиться и осциллирующие решения, напр.[math]
Интегрально-функциональное уравнение
А впрочем Лаплас в помощь, если известно, что у ограничена на бесконечности, тогда Лаплас точно берется (после отражения полуоси)
[math],
[math]
и тут что-то светит)
[math],
[math]
и тут что-то светит)
Интегрально-функциональное уравнение
Ian писал(а):Source of the post обращающаяся в 0 на - бесконечности
Если
Уравнение можно записать как
Отсюда видно, что
Если функция имеет конечный предел в
А если предел
Рассуждать можно как-то так:
Для любого
Тогда для всех
Кроме того из уравнения очевидно, что
Значит, если такая
Интегрально-функциональное уравнение
zykov писал(а):Source of the post А если пределв
равен
, то функция везде равна нулю.
Рассуждать можно как-то так:
Тот же
Это даже можно обобщить на случай, если
Интегрально-функциональное уравнение
Ian писал(а):Source of the post В МГУ на зачете предложили
Раз это зачет, а не олимпиада, то наверно там должно быть какое-то "ортодоксальное" решение через свойства
Может что-то вроде того, что
Интегрально-функциональное уравнение
Напомню, что это просто обозначение [math]
Из уравнения [math] следует непрерывность [math] и [math]. Точнее, раз уравнение удовлетворяется почти всюду, то почти всюду непрерывность, но в классе равных п.в. функций x(t) можно выбрать ту, что u(t) будет непрерывна. соответственно [math] будет непрерывна всюду, кроме 0. Это из теоремы об абсолютной непрерывности интеграла Лебега, в частности, непрерывности по переменному верхнему пределу, она есть в курсе.С дифференцируемостью п.в. правой части по t труднее,но это тоже верно(Колмогоров-Фомин,гл.VI,пар.1,п.3). А так как производная выразилась через непрерывную функцию -она доопределяется по непрерывности и диф.уравнение удовлетворяется всюду (кроме той точки, которая вначале была s=0, а потом ушла в бесконечность и не мешает)
Так что мне хочется понять, что же дает Лаплас. Нет ли такой программки, которая по изображению строит график неэлементарной функции -оригинала?
Из уравнения [math] следует непрерывность [math] и [math]. Точнее, раз уравнение удовлетворяется почти всюду, то почти всюду непрерывность, но в классе равных п.в. функций x(t) можно выбрать ту, что u(t) будет непрерывна. соответственно [math] будет непрерывна всюду, кроме 0. Это из теоремы об абсолютной непрерывности интеграла Лебега, в частности, непрерывности по переменному верхнему пределу, она есть в курсе.С дифференцируемостью п.в. правой части по t труднее,но это тоже верно(Колмогоров-Фомин,гл.VI,пар.1,п.3). А так как производная выразилась через непрерывную функцию -она доопределяется по непрерывности и диф.уравнение удовлетворяется всюду (кроме той точки, которая вначале была s=0, а потом ушла в бесконечность и не мешает)
Так что мне хочется понять, что же дает Лаплас. Нет ли такой программки, которая по изображению строит график неэлементарной функции -оригинала?
Интегрально-функциональное уравнение
Ian писал(а):Source of the post Так что мне хочется понять, что же дает Лаплас
Наверно те же
Интегрально-функциональное уравнение
Вобщем мне кажется, логика такая:
Раз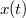 принадлежит
принадлежит 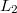 , то интеграл
, то интеграл 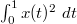 существует.
существует.
Значит предел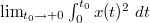 равен
равен 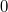 .
.
Значит в окрестности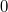 функция
функция 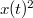 ограничена какой-то
ограничена какой-то 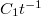 .
.
Значит в окрестности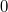 функция
функция 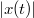 ограничена какой-то
ограничена какой-то 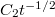 .
.
А как я уже показал
Из того, что в окрестности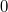 функция
функция 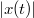 ограничена какой-то
ограничена какой-то 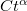 , где
, где 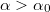 (а
(а 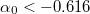 ), следует при условии выполнения интегрального уравнения, что
), следует при условии выполнения интегрального уравнения, что 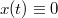 .
.
Есть вопросы к какому-то звену в цепочке? Нигде не ошибся?
Раз
Значит предел
Значит в окрестности
Значит в окрестности
А как я уже показал
zykov писал(а):Source of the post Это даже можно обобщить на случай, еслиограничена, где
, а
находится из уравнения
, численно
. (Т.е. пики
при приближении к нулю растут медленнее чем
, например если они растут как
.)
Из того, что в окрестности
Есть вопросы к какому-то звену в цепочке? Нигде не ошибся?
Интегрально-функциональное уравнение
zykov писал(а): интегралсуществует.
Значит ...
в окрестностифункция
ограничена какой-то
.
Вот этот переход неверен. функция может тотально прижиматься к 0 но иметь совсем узкие всплески, не ограниченные никакой степенной функцией [math]вообще.
Давайте я для рядов покажу, с ними проще пример.
покажем, что для любого [math] есть [math],(можете считать q=2) координаты которого сильно прорежены нулями, на котором [math]. Возьмем такое целое N, что [math] и положим [math],тогда [math]
а при [math], m -любое натуральное, [math]
Также бывают, например, несобственно-интегрируемые неотрицательные функции, не ограниченные на бесконечности, тоже со всплесками, не элементарные. Заменой переменной [math] превратятся в функции, не ограниченные [math] в нуле.
Последний раз редактировалось Ian 05 июн 2019, 03:47, всего редактировалось 1 раз.
Интегрально-функциональное уравнение
Да, я уже сам понял. Там могут быть узкие пики, которые дают малый вклад в интеграл.
Вобщем вместо этого шага нужно доказать (чтобы не уходить от интегралов и не иметь проблем с пиками), что из
Интегрально-функциональное уравнение
Что дает Лаплас в диф.-разн. уравнениях...ошибки он дает.
Уравнения [math] и [math] прекрасные тождества и в изображениях
А вот имеющее такое же решение [math] Лапласом решить не могу, там функции Хевисайда нужно вставлять а они разные
Уравнения [math] и [math] прекрасные тождества и в изображениях
А вот имеющее такое же решение [math] Лапласом решить не могу, там функции Хевисайда нужно вставлять а они разные
Интегрально-функциональное уравнение
Не знаю, как элегантно сделать.
Но через интеграл, как предел интегральной суммы получается так:
Если
Интегральная сумма для интеграла квадрата будет
Интегральная сумма для интеграла модуля будет
Значит
Т.е. если
Значит из интегрального уравнения в окрестности нуля функция
Значит, как было показано ранее, из интегрального уравнения следует что
Похоже, что задача решина.
Интегрально-функциональное уравнение
А, так это неравенство Коши_Буняковского
[math]
Действительно прошло, ура!
Задача, предложенная на зачете, была еще шире
Охарактеризовать спектр оператора
[math], но как все такие интегральные операторы, он компактен и спектр имеет не более одной сгущения (0 или нет), а как оператор Вольтерры (что обеспечивается наличием t в верхнем пределе) - не имеет ненулевых точек спектра вообще. Оставался вопрос 0-собственное значение или точка непрерывного спектра. Тогда уравнение [math] можно разок продифференцировать по t и останется то, что в посте 1.
[math]
Действительно прошло, ура!
Задача, предложенная на зачете, была еще шире
Охарактеризовать спектр оператора
[math], но как все такие интегральные операторы, он компактен и спектр имеет не более одной сгущения (0 или нет), а как оператор Вольтерры (что обеспечивается наличием t в верхнем пределе) - не имеет ненулевых точек спектра вообще. Оставался вопрос 0-собственное значение или точка непрерывного спектра. Тогда уравнение [math] можно разок продифференцировать по t и останется то, что в посте 1.
Интегрально-функциональное уравнение
Тут точно модуль?Ian писал(а):Source of the post,
Оператор то нелинейный получается...
Интегрально-функциональное уравнение
Да, без модуля
[math]
[math]
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Интегрально-функциональное уравнение
У этого уравнения есть еще свойство масштабной инвариантности: если 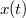 --- решение, то и
--- решение, то и 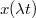 --- тоже решение.
--- тоже решение.
У дифференциального уравнения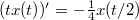 , на самом деле, целая куча степенных решений вида
, на самом деле, целая куча степенных решений вида 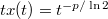 , где
, где 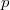 удовлетворяет уравнению
удовлетворяет уравнению
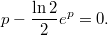
Помимо уже указанных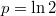 ,
,  , это уравнение имеет бесконечное множество решений, достаточно близких к
, это уравнение имеет бесконечное множество решений, достаточно близких к
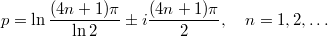
Эти решения осциллируют, но вещественная часть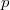 у них еще больше.
у них еще больше.
У дифференциального уравнения
Помимо уже указанных
Эти решения осциллируют, но вещественная часть
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 4 гостей