Олимпиада северных стран

Ian · Сообщение **Ian** » 02 май 2019, 14:11

Так вот, задача 3, оценка сверху. Жюри походя использует такое любопытное утверждение. Пусть А -некоторое множество в d-мерном пространстве.Рассмотрим Т- максимальный по объему симплекс (выпуклую оболочку (d+1) точки) с вершинами на множестве А. Рассмотрим центр тяжести S этой системы из (d+1) точки и симплекс T', гомотетичный Т относительно S c коэффициентом (-d). Тогда симплекс T', напротив, содержит множество А, благодаря той максимальности объема.

Ну, понятно для чего. Объем симплекса T' превосходит объем симплекса Т в

d^d=e^{d\ln d}=e^{o(d^2)} раз, и в то же время T' содержит выпуклую оболочку А. Поэтому достаточно оценить тот же определитель Вандермонда сверху.
И кто говорит, что это было легко

zykov · Сообщение **zykov** » 02 май 2019, 16:45

Ian писал(а):Source of the post В некоторую выпуклую кривую вписан максимальный по площади треугольник. Тогда треугольник, для которого стороны предыдущего являютися средними линиями - описан около этой кривой

А как доказать, что эта выпуклая кривая лежит полностью в этом большом треугольнике?
Вдруг она за его пределы вылезет...
(Ну и как их общее утверждение доказать про гомотетичный симплекс в d-мерном пространстве?)

zykov · Сообщение **zykov** » 02 май 2019, 18:29

peregoudov писал(а):Source of the post Седьмая заставляет вспомнить недавнюю находку zykov'а про конформные преобразования в круге.

Да, в задаче номер 7 тоже легко, если помнишь волшебную функцию $\frac{a-x}{1-\bar a x}$ ( $|a|<1$

), которая переводит круг в себя, $a$

переводит в $0$

, а

переводит в $a$

.

Для ясности, по шагам.
Сначала частный случай, когда $f(0)=0$

и

. Тогда неравенство принимает форму $|f'(0)| \leq 1$ .
Это легко доказать из принципа максимума, аналогично подходу Ian в той задаче 2016 года.

Ian писал(а):Source of the post тогда есть оценка $|f(z)| \leq |z|$ - доказательство: функция голоморфна и также не превосходит 1 на окружности, значит, в круге для нее применяем принцип максимума.

Если

и в единичном круге $|f(z)| \leq 1$ , то $f_1(z)=f(z)/z$

тоже голоморфна в единичном круге и $|f_1(z)| \leq 1$ в нём.
Тогда $f'(z)=f_1(z)+zf_1'(z)$

, значит

и $|f'(0)|=|f_1(0)| \leq 1$ .

Вторым шагом обобщим на произвольную $f(0) \neq 0$ .
Тогда для функции $g(z)=(f(0)-f(z)) \; / \; (1-\bar f(0) f(z))$ применимо неравенство из первого шага.
Учитывая $g'(z)=(f(0)\bar f(0)-1)f'(z) \; / \; (1-\bar f(0) f(z))^2$ получим $g'(0)=(f(0)\bar f(0)-1)f'(0) \; / \; (1-\bar f(0) f(0))^2=-f'(0) \; / \; (1-|f(0)|^2)$ .
Значит $\frac{|f'(0)|}{1-|f(0)|^2} \leq 1$ .

Третьим шагом аналогично обощим на $z \neq 0$ .
Рассмотрим функцию $h(z)$

, такую что $f(z)=h(\frac{z_0-z}{1-\bar z_0 z})$ , где $|z_0|<1$

.
Тогда $f'(z)=(z_0 \bar z_0 - 1) h'(\frac{z_0-z}{1-\bar z_0 z}) \; / \; (1 - \bar z_0 z)^2$ .
Значит $f'(z_0)=(|z_0|^2 - 1) h'(0) \; / \; (1 - \bar z_0 z_0)^2 = - \frac{h'(0)}{1-|z_0|^2}$ .
Следовательно $|f'(z_0)|=\frac{|h'(0)|}{1-|z_0|^2} \leq \frac{1-|h(0)|^2}{1-|z_0|^2} = \frac{1-|f(z_0)|^2}{1-|z_0|^2}$ .

zykov · Сообщение **zykov** » 02 май 2019, 19:22

Ian писал(а):Source of the post Жюри походя использует такое любопытное утверждение.

До этого решения тоже непонятно как додуматся - какая линия рассуждений.
Интересно, как студент Stanislav её решал.
Только он 9 балов получил за неё. Остальные максимум 5 балов - видимо сделали только нижнюю оценку с пирамидкой.

zykov · Сообщение **zykov** » 02 май 2019, 21:19

Задача номер 5 какая-то странная.
Никто из студентов не решил её. Только у Stanislav 6 из 10 и ещё у двух частичный бал менее 6.

По условию тоже непонятно. Упоминается $n$

, которое потом не используется. Видимо имелся ввиду размер матрицы.
Не сказано про домен - действительные или комплексные. "Симметричная матрица" конечно наводит на мысль о действительных. Для комплексных обычно самосопряженная. Но всё же лучше явно написать.

У меня как-то так получается:
$cR^{-1}-D^{-1}=R^{-1}(cE-RD^{-1})=R^{-1}(cD^{1/2}-RD^{-1/2})D^{-1/2}=$
$=R^{-1}D^{1/2}(cE-D^{-1/2}RD^{-1/2})D^{-1/2}$
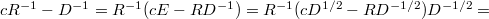
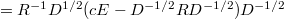
И аналогично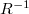 $R^{-1}$ можно вынести направо.
Значит неотрицательная определенность начальной матрицы эквивалентна неотрицательной определенности матрицы:
$cE-D^{-1/2}RD^{-1/2}$

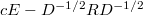
Матрица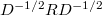 $D^{-1/2}RD^{-1/2}$ получается из матрицы $R$

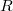масштабированием столбцов и строк на обратный корень из диагонального элемента.
Значит у этой матрицы будет единичная диагональ и она так же будет симметричной положительно определенной.
Т.е. без потери общности можно установить ограничение на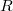 $R$

, что её диагональные элементы равны 1.
Тогда нужно найти минимальное $c$

, чтобы матрица $cE-R$

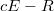была неотрицательно определенной.
Это минимальное $c$

равно максимальному собственному значению такой матрицы $R$

.
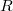Максимальное собственному значению такой матрицы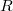 $R$

всегда меньша $n$

, т.к. след матрицы равен $n$

, значит сумма всех собственных значений равна $n$

, при этом каждое из них более нуля.

Ответ: минимальное $c$

равно

.
Экстремальный пример: матрица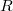 $R$

с единичной диагональню и недиагональнымим элементами равными 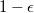$1-\epsilon$ , где $\epsilon$ - малая положительная величина. С уменьшением $\epsilon$ максимальное собственное значение такой матрицы приближается к $n$

.

zykov · Сообщение **zykov** » 02 май 2019, 22:46

zykov писал(а):Source of the post Значит неотрицательная определенность начальной матрицы эквивалентна неотрицательной определенности матрицы:
$cE-D^{-1/2}RD^{-1/2}$

Там есть тонкости со знакоопределенностью произведения матриц.
Так что лучше это по другому переписать.
Пусть $M=D^{-1/2}RD^{-1/2}$ , тогда $R=D^{1/2}MD^{1/2}$ .
И тогда
$cR^{-1}-D^{-1}=c(D^{1/2}MD^{1/2})^{-1}-D^{-1}=$
$=cD^{-1/2}M^{-1}D^{-1/2}-D^{-1}=D^{-1/2}(cM^{-1}-E)D^{-1/2}$

Значит $cR^{-1}-D^{-1}$ положительно определенная тогда и только тогда, когда $cM^{-1}-E$ положительно определенная.
(Смотри wikipedia: Definiteness of a matrix Multiplication.
"If M and N are positive definite, then the products M N M and N M N are also positive definite.")

Ian · Сообщение **Ian** » 03 май 2019, 07:31

zykov писал(а):
Ian писал(а):Source of the post В некоторую выпуклую кривую вписан максимальный по площади треугольник. Тогда треугольник, для которого стороны предыдущего являютися средними линиями - описан около этой кривой

А как доказать, что эта выпуклая кривая лежит полностью в этом большом треугольнике?
Вдруг она за его пределы вылезет...
(Ну и как их общее утверждение доказать про гомотетичный симплекс в d-мерном пространстве?)

Кстати, выпуклость не обязательна, просто картинка красивее- один треугольник весь внутри, другой весь снаружи. Рассмотрим любую сторону Р (грань, гипергрань), проведенную через d точек, тогда ее образ P' при гомотетии параллелен ей и проходит через оставшуюся вершину.Но из максимальности объема, та вершина была самая удаленная от Р точка, значит все исходное множество лежит по ту же сторону от P' что и центр тяжести. И так для каждой стороны(грани,гиперграни)

zykov · Сообщение **zykov** » 03 май 2019, 16:59

Понятно.
Ну так нужно для этой спирали найти этот симплекс с максимальным объёмом и доказать, что этот объем максимален.
Ту пирамидку, что Вы нашли (для нижней оценки), у неё же объём не максимален.

zykov · Сообщение **zykov** » 03 май 2019, 23:00

Я к тому, что найти этот симплекс с максимальным объёмом или просто оценить сверху его объем - тоже непростая задача.
Так что у меня возникают сомнения, есть ли у авторов самих правильное решение...
(А то может решение есть, но оно неправильное.)

Ian · Сообщение **Ian** » 04 май 2019, 09:44

Объем d- мерного симплекса

w_d -это модуль определителя Вандермонда, деленный на d!, значит, для любых

0\leq x_0<x_{1}<...<x_{d}\leq1

w_{d}=\frac{1}{d!}|\begin{vmatrix}1 & x_{0} & ... & x_{0}^{d}\\
\vdots &\vdots & ... & \vdots\\
1 & x_{d} & ... & x_{d}^{d}
\end{vmatrix}|=\frac{1}{d!}\prod_{i>j\geq 0}|x_{i}-x_{j}|
Среднее арифметическое перемножаемых модулей не больше 1/2 асимптотически. Близко к 1/2,когда точки раскиданы пополам одни близки к 0, другие к 1. Тогда и их среднее геометрическое не больше 1/2 асимптотически

w_d\leq (0,5+\varepsilon)^{d(d+1)/2}, а значит, и для

v_d есть такая же оценка
Итак, оценка сверху далась с еще меньшими вычислениями, но труднее идейно

zykov · Сообщение **zykov** » 09 май 2019, 07:24

Похоже, что все задачи кроме номер 3, довольно простые.
В номер 3 тоже не очень сложно, если уже знаком с этим приёмом - "симплеск максимального объема и ему подобный симплекс".
Мне вот интересно, этот факт - это что-то хорошо известное в какой-то области математики?

Ian · Сообщение **Ian** » 09 май 2019, 10:13

zykov писал(а):В номер 3 тоже не очень сложно, если уже знаком с этим приёмом - "симплеск максимального объема и ему подобный симплекс".
Мне вот интересно, этот факт - это что-то хорошо известное в какой-то области математики?

Я только за себя могу сказать).Учился-учился. а узнал вот только в эти дни...Хуже когда забываю приемы, которым сам же учил на старом форуме (см. новую тему)

Портал Естественных Наук, версия 1.1