Портал Естественных Наук, версия 1.1

Утащил с dxdy, где ничего путного не написали и даже немного наговорили глупостей. А задачка мне показалась интересной.

Найти сферически-симметричные решения уравнения

$\Delta u+u^n=0.$

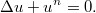
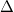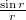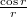$\Delta$ --- трехмерный лапласиан. Пусть n будет натуральным и нечетным. В линейном случае n=1, например, решениями являются $\frac{\sin r}r$ и $\frac{\cos r}r$ . Будут ли решения при других n похожи на эти?

\frac 1{r^2}\frac d{dr}\left( r^2\frac{du}{dr}\right) +u^n=0

\frac {d^2u}{dr^2}+\frac 2r\frac{du}{dr}+u^n=0
Именно при

n\ne 1 имеется однородное решение

C_nr^{2/(1-n)}, проверяемое подстановкой. Про другие решения не думал

При

это решение вырождается в $u(r)=0$

.

C_{n}=\left[\frac{2}{n-1}\left(1-\frac{2}{n-1}\right)\right]^{\frac{1}{n-1}}

C_3=0 случай с n=3 наиболее мутный

На википедии такое есть: Lane–Emden equation.

Ну вот и на dxdy наибольшие терки были по поводу n=3... Википедия --- это не спортивно. На мой взгляд, тут довольно элементарными методами можно исследовать качественное поведение решений при любых n. Первый шаг Ian уже фактически сделал.

На вики написано, что аналитические решения есть только для $n=0,1,5$

.
Там видимо имеется ввиду граничное условие $u(0)=u_0$

(конечное), $u'(0)=0$

.
(Без потери общности при $n\neq 1$ можно положить $u_0=1$

просто изменяя масштаб $u$

и

.)
Решения Ian в нуле стремятся к бесконечности при $n>1$

, так что не подходят.

Так что, можно уточнить, что имеется ввиду?

peregoudov писал(а):Source of the post Найти сферически-симметричные решения уравнения

Аналитических там больше нет.
В виде ряда легко представить. Нечётные производные равны нулю, $u''(0)=-u_0^n/3$

и дальше производные 4ой, 6ой и т.д. степеней в нуле находятся из того же уравнения.

Замена независимой переменной

r=\frac 1t упрощает уравнение. А что узнать-то хотели

t^4\frac{d^2u}{dt^2}=-u^n

Вроде при

при больших $r$

оно похоже на $\frac{\sin(2^{1/4} \sqrt r)}{2^{1/4} \sqrt r}$ .
В нуле он $1-\frac{{{r}^{2}}}{6}+\frac{{{r}^{4}}}{40}-\frac{19 {{r}^{6}}}{5040}+\frac{619 {{r}^{8}}}{1088640}-\frac{17117 {{r}^{10}}}{199584000}+\frac{1208293 {{r}^{12}}}{93405312000}+\mbox{...}$ .

Кажется. кроме n=3 они осциллирующие
https://www.wolframalpha.com/input/?i=s ... %29%29%5E5
А при n=3 осциллируют не все
https://www.wolframalpha.com/input/?i=s ... %29%29%5E3

Вроде нечётные осцилируют, а чётные нет.
3: https://www.wolframalpha.com/input/?i=s ... Bf%5E3%3D0
4: https://www.wolframalpha.com/input/?i=s ... Bf%5E4%3D0

Я думаю, следует прежде всего ставить задачу качественного исследование решений. Если этого не сделано, то и разложение построить не получится. А качественно исследовать мы хорошо умеем автономные уравнения...

zykov писал(а):Source of the post Вроде при при больших оно похоже на $\frac{\sin(2^{1/4} \sqrt r)}{2^{1/4} \sqrt r}$ .

Если сделать замену переменных $t = 2^{1/4} \sqrt r$ и $u(r) = \frac{f(t)}{t}$ , то уравнение будет $f''+f'/t+2f^3-f/t^2=0$

.
Если предположить, что $f(t)$

- что-то вроде синуса, амплитуда которого не слишком быстро убывает (чтобы $f^3$

падал не слишком быстро), то можно оставить только $f''+2f^3=0$

.
Тут решение конечно не синус (из-за куба), но на него похоже.
Тоже что-то периодическое с постоянной амплитудой.
(Нелинейные колебания на пружине, где возвращающая сила пропорциональна кубу сдвига. Потенциальная яма 4-ой степени.)

Нестационарная сила линейного отталкивания $f/t^2$

даёт малый вклад. Возможно как-то несильно и повлияет на амплитуду.
Для линейной по скорости силы трения $-f'/t$

коэффициент трения линейно падает по времени.
За один период она отъест $\overline{(f')^2} \frac{T}{t}$ энергии.
Т.е. по идее энергия должна падать как $t^{-1}$ (тут правда в отличии от линейного осцилятора $\overline{(f')^2}$ может быть не пропорционален энергии - нужно проверить).
Тогда амплитуда будет падать как $t^{-1/4} \sim r^{-1/8}$ .
Т.е. для $u$

амплитуда будет падать не как $r^{-1/2}$ , а как $r^{-5/8}$ .
Ну и частота осциляций будет менятся, т.к. для нелинейного осцилятора период колебаний зависит от амплитуды.

На самом деле тут нужна другая замена переменных. Ее идея состоит в рассмотрении того масштабного преобразования, которое оставляет уравнение инвариантным: $r\to\lambda r$ , $u\to\lambda^{-2/(n-1)}u$ . Если перейти к переменным $t=\ln r$ , $v=r^{2/(n-1)}u$ , то в новых переменных преобразование принимает вид $t\to t+\ln\lambda$ , $v\to v$ . То есть в новых переменных уравнение будет инвариантным относительно сдвига $t$

, другими словами, автономным. В явном виде

$v''+\frac{n-5}{n-1}v'-\frac{2(n-3)}{(n-1)^2}v+v^n=0.$

Отсюда сразу видно, чем выделен случай n=5: получается нелинейный маятник с потенциалом в форме "жопы Лифшица". Решение Ian'а $\sim r^{-1/2}$ соответствует одному из минимумов, а указанное в википедии $\sim(1+r^2)^{-1/2}$ --- сепаратрисе.

peregoudov писал(а):Source of the post На самом деле тут нужна другая замена переменных.

Какая замена нужна - зависит от целей...

zykov писал(а):Source of the post (тут правда в отличии от линейного осцилятора $\overline{(f')^2}$ может быть не пропорционален энергии - нужно проверить).

Есть подозрение, что для такого осцилятора $\overline{(f')^2}$ пропорционально энергии в степени $3/4$

. Тогда энергия падает до 0 за конечное время (хотя это время и растёт экспоненциально).
Тогда правда слагаемое $f/t^2$

может помешать занулению.

Да, если вернутся к исходному уравнению $u''+2u'/r+u^3=0$

, то это тот же осцилятор в поле 4-ой степени с линейным по скорости трением (коэффициент трения падает как "-1" степень со временем).
Форма осциляций само собой негармоническая.
Амплитуда падает как $c - k\ln r$ , т.е. падает до 0 за конечное время (экспоненциальное по начальной амплитуде). По мере падения амплитуды период колебаний растёт как "-1" степень амплитуды. Т.е. возможно нуля оно и не достигнет, если период колебаний уйдёт в бесконечность.

Всё же пока не понятно, как оно приближается к нулю на бесконечности при этом загадочном $n=3$

...

Тут вот в чём может быть дело.
Сам результат $\dot E \sim -E^{3/4}$ основан на усреднении потери энергии на трение по одному периоду.
Для этого сам период должен быть малым, чтобы за один период терялась малая доля энергии.
Но если при малой амплитуде период становится большим, то это уже не верно.
Т.е. нужно анализировать детальнее при малой амплитуде.

Я, конечно, не претендую на точную оценку при $r\to\infty$ , но грубую сделать нетрудно. При n=3 уравнение в моих переменных принимает вид

$$ v''-v'+v^3=0. $$

При этом

. Функцией Ляпунова для такого уравнения, очевидно, будет $L=\frac{v^{\prime2}}2+\frac{v^4}4$ . Имеем $L'=v^{\prime2}\leq 2L$ , а потому $L\leq c_1e^{2t}$ . Значит $|v|\leq(4L)^{1/4}\leq c_2e^{t/2}=c_2\sqrt r$ . То есть при больших r имеем $|u|\leq c_2r^{-1/2}$ .

Гораздо труднее оценить поведение при $r\to0$ .

Тоже решил посмотреть в Ваших переменных.
Тут тот же нелинейный осцилятор в яме 4-ой степени. Только теперь "антитрение" линейное по скорости с постоянным коэффициентом трения.
Это "антитрение" будет разгонять осцилятор. Энергия должна расти как $t^4$