Страница 1 из 1
Пять квадратиков
Добавлено: 14 фев 2021, 07:24
Ian
При каком наименьшем [math]a в квадрате со стороной [math]a можно разместить 5 единичных квадратиков?
Пять квадратиков
Добавлено: 14 фев 2021, 09:52
ARRY
Без незаполненного пространства, естественно, не получится (только если
[math]n - полный квадрат).
А с незаполненным пространством эта задача рассматривалась, если память не изменяет, в одном из древних "Квантов".
Некоторые результаты есть
здесь.
Пять квадратиков
Добавлено: 14 фев 2021, 16:17
Ian
Спасибо, интернет-олимпиада, решение одной из задач которой есть в википедии, это недоработка конечно
Пять квадратиков
Добавлено: 14 фев 2021, 23:44
ARRY
Да это ещё полбеды, в Википедии, особенно русской, немало ляпов, а то и грубых ошибок.
Гораздо хуже, что организаторы олимпиады вместо составления новых задач берут уже известные из олимпиад 30-40-50-летней давности. А опытные олимпиадники с этими задачами обязаны быть знакомы.
Пять квадратиков
Добавлено: 15 фев 2021, 09:42
Ian
С другой стороны, двадцатилетние не знакомы ни с чем, что было общеизвестно и популярно 20 лет назад. Видимо потому что на них катится такой объем свежей информации, что просто некогда о старом почитать. Пусть хоть так, но чтобы решение не находилось поиском в гугле.
А надо отметить что у этой олимпиады задачи были со вкусом(не знаю кто проводил): соседняя тема про сумму ряда, или вот

- circ.png (82.37 KiB) 14826 просмотра
Тут уж не все догадаются, что поиском надо искать слово "циркулянт"
Пять квадратиков
Добавлено: 15 фев 2021, 14:04
zykov
Если там не требовалось доказательства, а только нужно было ввести целое число в веб-форму, то там думать вообще не надо - просто на компьютере просуммировал несколько первых слагаемых и округлил до целого. Можно за одну минуту уложиться.
Пять квадратиков
Добавлено: 15 фев 2021, 14:09
zykov
Про 5 квадратов, то глядя на картинку - довольно очевидно, что меньше нельзя. Но вот как это строго доказать? Как-то не просто...
Пять квадратиков
Добавлено: 15 фев 2021, 14:55
zykov
Ian писал(а):Source of the post Тут уж не все догадаются, что поиском надо искать слово "циркулянт"
Тут какая-то глубокая теория про циркулянт не требуется. Даже школьник знакомый с системами линейных уравнений может решить (учитывая симметрию в этой системе).
Наприме вычитая из второго равенства первое получаем
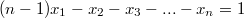
.
Аналогично можно сделать для
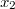
и
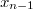
.
Для
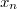
похожим образом из первого нужно вычесть последнее. Получиться
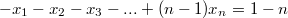
.
Если сложить эти 4 новых равенства, то будет
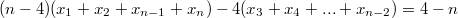
.
С другой стороны, если сложить все равенства вместе, то будет
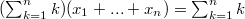
.
Т.е.
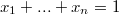
.
Подставляя это в предыдущее равенство получаем
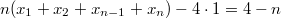
.
В итоге
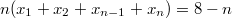
.
Пять квадратиков
Добавлено: 15 фев 2021, 18:19
zykov
Это можно получить короче, если сразу вычесть из тертьего равенства предпоследнее равенство.
Но выделять по одному слагаемому за раз - более интуитивно.
Пять квадратиков
Добавлено: 15 фев 2021, 19:07
Ian
Я решил систему, но теория про циркулянт использована только в том смысле что он отличен от 0, и значит подобранное решение единственно. Ясно что если в правой части столбец перевернутый; n,n-1,...1, то [math]x_n=1, остальные нули. А если в правой части столбец из равных чисел, например чисел [math](n+1), то и [math]x_i все равны и легко найти какие. Вычитая из второго решения первое, получим решение всей данной системы.
Пять квадратиков
Добавлено: 15 фев 2021, 20:32
zykov
Да, найти все

тоже можно.
(Достаточно найти

для нескольких небольших

, а там тенденция уже видна - все кроме последнего равны друг другу, а сумма всех равна 1.)
Но думаю, имелось ввиду найти эту сумму не находя сами

.
Пять квадратиков
Добавлено: 21 фев 2021, 22:33
peregoudov
А к какой-нибудь задаче линейного программирования "пять квадратиков" не сводятся? Задать неравенствами пять квадратиков и большой квадрат, попадание маленького квадратика внутрь большого и во внешность остальных маленьких --- какие-то логические конструкции из неравенств...
Пять квадратиков
Добавлено: 22 фев 2021, 00:47
zykov
"Сложный" путь доказательства оптимальности в лоб там конечно есть. Но это уже скорее дело для компьютера.
Правда чисто линейное програмирование наверно не пройдёт из-за поворотов.
Я имел ввиду, есть ли сравнительно несложный метод руками в тетрадке?
Пять квадратиков
Добавлено: 22 фев 2021, 00:56
zykov
Кстати, насчёт поворотов.
У меня тут есть парочка металлических пазлов
Hanayama.
Там нужно сцеплять/расцеплять твёрдые фигуры. Довольно сложно - рекомендую, если такое интересно.
Всё думал, как программу написать, чтобы решала такой пазл. Честно говоря, оно не просто. Пока даже не знаю как, хотя должно быть решаемо.
Там тоже 3D повороты усложняют дело.
Если фигуры имеют форму многогранников, то должно быть попроще. Но есть фигуры и кривой формы, причём не всегда часть окружности (шара или цилиндра).
.