Некоторое испытание может давать n равновероятных результатов. Проводится n испытаний. Пусть k-случайная величина, число различных результатов в n испытаниях . Найти матожидание отношения k/n
Для n=100 сегодня задача об этом была предложена на некоторой IT- олимпиаде. Может, хотели чтобы численно нашли. У меня ответ 0,6339676587
А как она ведет при n, асимптотика, форма распределения
Матожидание числа различных результатов
Матожидание числа различных результатов
Можно решать через Марковские процессы, аналогично теме Вероятность определённой последовательности.
Пусть у нас вектор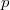 - вектор длины 100 содержащий вероятности того что было такое-то количество различных результатов.
- вектор длины 100 содержащий вероятности того что было такое-то количество различных результатов.
После первого испытания у нас 100% вероятности, что есть ровно 1 различный результат. Т.е. вектор везде равен нулю, кроме первого элемента равного единице (вектор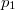 ).
).
Если после какого-то количества испытания у нас разных результатов, то после ещё одного испытания будет
разных результатов, то после ещё одного испытания будет  разных результатов с вероятность
разных результатов с вероятность 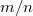 , и будет
, и будет 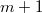 разных результатов с вероятность
разных результатов с вероятность 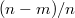 .
.
Т.е. столбец вектор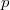 слева умножается на матрицу
слева умножается на матрицу 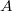 , в которой ненулевые только главная диагональ и её соседняя диагональ снизу.
, в которой ненулевые только главная диагональ и её соседняя диагональ снизу.


После 100 испытаний вектор вероятностей будет:
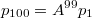
Зная вектор вероятностей легко найти матожидание количества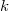 - просто умножить его слева на строку
- просто умножить его слева на строку 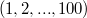 .
.
(Видимо то, что имелось ввиду на IT- олимпиаде.)
Пусть у нас вектор
После первого испытания у нас 100% вероятности, что есть ровно 1 различный результат. Т.е. вектор везде равен нулю, кроме первого элемента равного единице (вектор
Если после какого-то количества испытания у нас
Т.е. столбец вектор
После 100 испытаний вектор вероятностей будет:
Зная вектор вероятностей легко найти матожидание количества
(Видимо то, что имелось ввиду на IT- олимпиаде.)
Последний раз редактировалось zykov 01 апр 2020, 22:00, всего редактировалось 3 раз.
Матожидание числа различных результатов
В Maxima посчитал точное значение матожидания количества 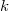 (точная десятичная дробь):
(точная десятичная дробь):
Код: Выбрать все
63.396765872677049506938397342748261381028792336107630859404262730068295524927525181280345648997304959933843089934715672528176430319820058414289464550829242572610964993901729162885021780083239150509999Матожидание числа различных результатов
Забавно. Получилось найти точную формулу.
Матожидание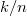 точно равно
точно равно  .
.
Матрица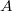 имеет простые собственные значения и собственные вектора.
имеет простые собственные значения и собственные вектора.
Собственные значения: 1,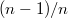 ,
, 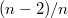 , ...,
, ..., 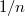 .
.
Им соотвествуют собственные вектора с ненулевыми значениями в конце равными биномиальным коэффициентам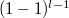 .
.
Например первый вектор в конце имеет 1. Второй имеет (1, -1). Третий - (1, -2, 1). Четвертый - (1, -3, 3, -1). И т.д..
Удобно, чтобы знак единицы в последней строке чередовался. Тогда, если объединить эти столбцы в матрицу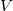 , то ей обратная матрица
, то ей обратная матрица 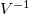 тоже имеет простую форму. Её первый столбец состоит из биномиальных коэффициентов
тоже имеет простую форму. Её первый столбец состоит из биномиальных коэффициентов 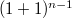 . Начало второго столбца состоит из биномиальных коэффициентов
. Начало второго столбца состоит из биномиальных коэффициентов 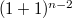 . И т.д.. Последний столбец имеет только один ненулевой элемент - 1 в начале.
. И т.д.. Последний столбец имеет только один ненулевой элемент - 1 в начале.
Умножение столбца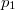 слева на матрицу
слева на матрицу 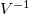 даёт её первый столбец - столбец состоящий из биномиальных коэффициентов
даёт её первый столбец - столбец состоящий из биномиальных коэффициентов 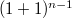 .
.
Интересно, что умножение строки справа на матрицу
справа на матрицу 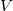 даёт строку в которой только первые два элемента ненулевые и равны
даёт строку в которой только первые два элемента ненулевые и равны  .
.
Это позволяет найти точный ответ для матожидания количества разных результатов в виде:

Матожидание
Матрица
Собственные значения: 1,
Им соотвествуют собственные вектора с ненулевыми значениями в конце равными биномиальным коэффициентам
Например первый вектор в конце имеет 1. Второй имеет (1, -1). Третий - (1, -2, 1). Четвертый - (1, -3, 3, -1). И т.д..
Удобно, чтобы знак единицы в последней строке чередовался. Тогда, если объединить эти столбцы в матрицу
Умножение столбца
Интересно, что умножение строки
Это позволяет найти точный ответ для матожидания количества разных результатов в виде:
Матожидание числа различных результатов
Ian писал(а):Source of the post А как она ведет при n, асимптотика, форма распределения
В пределе, понятно, будет
Ряд Лорана на бесконечности будет
Матожидание числа различных результатов
Вот вопрос, как просто найти этот простой ответ?
Матожидание числа различных результатов
Особенно забавен путь которым она найдена. Должно же быть вероятностное доказательство этого.zykov писал(а):Забавно. Получилось найти точную формулу.
Матожиданиеточно равно
.
Также дисперсию распределения k считаю численно, она в разы меньше чем у биномиального распределения с таким матожиданием (пик острее)
P.S.
Это можно принять за определение числа e: пусть разбрасывается огромное число n предметов по n ячейкам: ожидаемое отношение n к числу пустых ячеек
Матожидание числа различных результатов
Ian писал(а):Source of the post Также дисперсию распределения k считаю численно, она в разы меньше чем у биномиального распределения с таким матожиданием (пик острее)
Через матрицу можно посчитать матожидание для
Отсюда для дисперсии
(примерно
Ряд Лорана на бесконечности:
(Т.е. примерно
Матожидание числа различных результатов
Ian писал(а):Source of the post Должно же быть вероятностное доказательство этого.
Ну это доказательство вполне вероятностное...
Исходя из вероятностных рассуждений мы получили связь в матричной форме. Потом провели алгебраические преобразования в этой форме. Интересно, что результат сам собой сильно упростился. Наверно тут должна быть какая-то причина...
zykov писал(а):Source of the post Это позволяет найти точный ответ для матожидания количества разных результатов в виде:
Для полноты, этот результат справедлив для любого количества испытаний (не только для
Для
Например, если брать
Матожидание числа различных результатов
Ой какое простое рассуждение
[math], где случайная величина [math] тогда и только тогда, когда m-й из результатов получен хоть в одном испытании, иначе 0
[math]- как у начинающих
открывая тему, я почему-то верил , что доля k/n стремится к 0, интуиция подвела
[math], где случайная величина [math] тогда и только тогда, когда m-й из результатов получен хоть в одном испытании, иначе 0
[math]- как у начинающих
открывая тему, я почему-то верил , что доля k/n стремится к 0, интуиция подвела
Матожидание числа различных результатов
Там многие задачи на рекуррентности, и поэтому я тоже не сомневаясь начал с них и нашел ответ. Его сложность и сбила с толку
Вот например viewtopic.php?f=4&t=1160 пришлось открыть другую тему
Вот например viewtopic.php?f=4&t=1160 пришлось открыть другую тему
Матожидание числа различных результатов
Да, верно.
Хотя разные случайные величины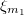 и
и 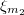 не являются независимыми, но это никак не влияет на то что матожидание суммы равно сумме матожиданий.
не являются независимыми, но это никак не влияет на то что матожидание суммы равно сумме матожиданий.
Хотя разные случайные величины
Матожидание числа различных результатов
А вот эту дисперсию уже иначе было не найтиzykov писал(а):Отсюда для дисперсииполучается:
(примернопри
.)
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей