Ian писал(а):Source of the post Но теперь то, что некоторая переменная независящая ни от одной свободной -это свойство самой матрицы 25х25, интересно какая это переменная из 25ти
Не очень понимаю о чём речь...
Может это как-то математически однозначно выразить?
Собственно, что мы тут делаем. У нас есть линейное уравнение в
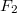
в виде
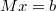
.
Здесь
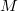
- это матрица системы 25x25 (какие ламочки меняют состояние при нажатии кнопок).
Вектор

- это вектор нажимаемых кнопок (для них в нём "1").
Вектор

- это вектор начального состония которое нужно занулить (или, что эквивалентно, конечное состояние, которое мы хотим получить из нулевого).
Для данного

система может быть несовместной, т.к. ранг матрицы
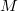
не полный. Тогда решений нет.
Или система может быть совместной, тогда мы можем найти

.
Как мы это делаем? Мы факторизуем матрицу
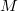
в произведение нижней треугольной матрицы и верхней треугольном матрицы -
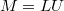
. Делаем это методом Гаусса.
Здесь
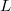
- это нижняя треугольная матрица с полным рангом. На её главной диагонали только единицы.
Так же
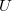
- это верхняя треугольная матрица. Её ранг такой же, как у матрицы
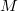
. В ней верхние строки ненулевые (количество этих строк равно рангу - у нас 17). В этих строках на главной диагонали только единицы. Оставшиеся нижние строки нулевые (их количество у нас 25-17=8).
Тут ещё такой момент, чтобы получить эти матрицы именно в таком виде, скорее всего нам понадобится поменять порядок элементов в векторах

и

.
Как идёт метод Гаусса? Сначала мы вычитаем первое уравнение их всех остальных, так чтобы во всех кроме первого отсутствовала первая переменная. Таким образом мы зануляем первый столбец ниже главной диагонали для
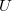
. А изменения в

при этом процессе отражаются в матрице
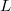
(в её первом столбце). Потом тоже делаем со вторым столбцом для уравнений с третьего и до конца. И т.д.
Но чтобы провести такую процедуру, текущая строка должна сама зависеть от удаляемой переменной. Т.е. в текущем состоянии на главной диагонали должна быть единица. Но иногда там оказывается ноль (после предыдущих удалений). Тогда в этом столбце ниже главной диагонали мы ищем ненулевой элемент и меняем эти строки местами - т.е. делаем перестановку элементов

. Но может оказатся, что в этом столбце ниже главной диагонали только нули (для этой матрицы ранга 17 так 2 раза оказалось). Тогда мы ищем ненулевой элемент в следующих столбцах и меняем ещё и столбцы местами. Это значит, что мы меняем порядок элементов в векторе

.
В итоге, мы заменяем нашу систему на две системы -
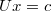
и
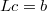
.
Из

легко получить

(и обратно) через матрицу
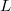
.
Когда система несовместна? Когда хотя бы один из 8 последних элементов в

ненулевой. В качестве базиса можно выбрать, чтобы ровно один из восьми был единицей. Тогда все остальные получаются из них нетривиальными линейными комбинациями. Если каждый из этих базисных векторов умножить на
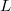
, то получим базис в пространстве для

.
Какие нажатия кнопок не меняют в итоге состояние лампочек? Это такие

для которых
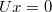
.
В матрице
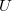
левый верхний квадрат 17x17 является верхней треугольной матрицей, у которой только единицы на главной диагонали. Значит для последних 8 переменных в векторе

мы можем выбрать любые значения (чтобы только не все нули), умножить их на 8 последних столбцов в матрице
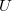
и перенести результат в правую часть. Получим уравнения для первых 17 переменных в

, которое решается легко (в силу треугольности матрицы) и однозначно (в силу полноты ранга матрицы 17x17).
Я так понимаю, эти последние 8 переменных - это Ваши независимые переменные.
А первые 17 - это Ваши зависимые.
Выбирая восемь вариантов этих 8 переменных, так чтобы только одна была "1" и решая уравнение для оставшихся 17 мы можем найти базис нуль-пространства в

. Я его приводил.
С другой стороны мы можем положить все 8 равными нулю - т.е. запретить их нажимать. И все равно любая совместная система будет разрешима. Я тоже приводил, какие 8 можно запретить нажимать.
Есть ли другие такие восьмерки? Из симметрии видно, что точно есть.
Перед факторизацией мы можем переставить

и

как угодно и начать факторизацию с другого элемента в
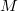
. В процессе факторизации скорее всего мы опять будем менять порядок в

и

, но вполне возможно, что в результате какая-то другая восьмерка окажется в конце вектора

.
Насчет того, что мы можем выбрать любые 3 кнопки и они войдут обязательно в какую-то восьмерку, и что есть четверки кнопок не входящие ни в одну восьмерку. Тут я не вижу возможности это получить из только одной
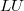
факторизации. Я это делал брут-форс перебором.