Портал Естественных Наук, версия 1.1

Здраствуйте. При разборе этой задачи возник у меня вопрос, который сейчас оформился в самостоятельную задачу.
Предположим, что игральную кость бросают много раз, скажем, 200. Какова вероятность, что хотя бы раз выпадет последовательность 1,2,3,4,5,6 ?
Как подступиться к такой задаче?

Dolly писал(а):Source of the post Как подступиться к такой задаче?

Посчитать количество подходящих вариантов и поделить на .

Думаю, что точно это не выразить в простой форме.
А вот приближенно оценить это не сложно. Учитывая, что вероятность выпадение такой последовательности начиная с первого элемента равна - т.е. велична очень маленькая, можно отбросить более высокие порядки (выпадение последовательности более одного раза). Тогда приближенная оценка итоговой вероятности (195 случаев объедененных по "или") будет ().
Это оценка сверху.

zykov писал(а):195 случаев объедененных по "или"

zykov
А Вы можете расшифровать эту фразу? Не поняла.

Последовательность "начинается с 1" или "начинается с 2" или "начинается с 3" или ... или "начинается с 194" или "начинается с 195".
(Ещё раз повторю, что сумма этих вероятностей равна нужной вероятности не точно, а приближенно, т.к. события не являются независимыми.)

1) мне кажется, формула включений-исключений тут в лоб не идет, если знаете как -покажите.
2) однако рекуррентность 6-го порядка тут, кажется, возможна.Используем то, что 123456 не имеет в конце начала самой себя.
Обозначим [math]p_n вероятность наличия хоть одной "123456" в последовательности n бросаний.
Все последовательности n бросаний разобьем на 2 непересекающиеся группы -начинающиеся с 1 и иные Вероятность иных, годящихся нам [math]5*6^{-1}p_{n-1} . Среди начинающихся с 1 опять 2 случая -продолжаются 2-кой или иные. Тут вероятность иных, но годящихся нам опять известна [math]5*6^{-2}p_{n-2}, прем дальше...

И что получается?

Например вот это:
При будет .
При будет .
Это неверно. Это грубая оценка снизу. ()

В этой формуле не все случаи учтены (например первый элемент равен 1, но последовательность начинается не с первого элемента).
А если попробовать учесть все случаи, то сложно избавится от двойного учёта (когда например одна и та же последовательность учтена несколько раз - в и в ).

Вообще:
При будет .
При будет .
Дальше сложнее.

И так далее, с каждым шагом сложнее.

Точный ответ будет имееть сложную форму. Но как я ранее писал, пока , ответ хорошо оценивается как .

Ответ стремится к 1. И даже интересно, что это за формула, где ответ стремится к 1
Похожие задачи были в "Конкретной математике" но не могу найти. Рекуррентная формула и производящая функция чисел [math]p_n (это не распределение вероятностей!) точно есть какие-то

Ian писал(а):Source of the post И даже интересно, что это за формула, где ответ стремится к 1

Ну можно взять другую оценку - через "И": .
Она и при неплохо даёт. А при больших даёт правильную асимптотику.

Ну ведь с точки зрения человека сидящего и просматривающего последовательность слева направо все ясно. он может находиться только в 6 состояниях: ждет начала комбинации, 1цу; только что была 1ца. ждет 2ки; ...только что было 12345, ждет 6, или перейдет в состояние 0 с вер 2/3, или в состояние 1 с вер 1/6.
таким образом строка из 6ти вероятностей состояний по-марковски пересчитывается только через предыдущую. Ну у меня это ексель делает за секунду. Получилось 0,004171289<[math]195\cdot 6^{-6}=0,004179527
За n бросаний [math]p_nравно последней координате 7-мерного вектора
[math]\begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0 & 0\end{pmatrix}\begin{pmatrix}\frac{5}{6} & \frac{1}{6} & 0 & 0 & 0 & 0 & 0\\
\frac{2}{3} & \frac{1}{6} & \frac{1}{6} & 0 & 0 & 0 & 0\\
\frac{2}{3} & \frac{1}{6} & 0 & \frac{1}{6} & 0 & 0 & 0\\
\frac{2}{3} & \frac{1}{6} & 0 & 0 & \frac{1}{6} & 0 & 0\\
\frac{2}{3} & \frac{1}{6} & 0 & 0 & 0 & \frac{1}{6} & 0\\
\frac{2}{3} & \frac{1}{6} & 0 & 0 & 0 & 0 & \frac{1}{6}\\
0 & 0 & 0 & 0 & 0 & 0 & 1
\end{pmatrix}^{n}
, соответствующего вероятности попадания в поглощающее состояние 6

Действительно, Марковские процессы тут подходят.
И точный ответ выражается в виде степени матрицы 7x7.

Maxima даже выдала точный ответ:

Код: Выбрать все

49455865799704940506821264626539171368699137079061080677701284300232222955810860691117054263203303596926497244617241443485895725320102191217768409090323 / 11856256217000761133249302542188159231749687370958039708207752192642025820822770528307559426132141591578133762963225828637624034458822090066222655331106816

примерно 0.00417129

У матрицы 7x7 собственные значения: 1, 0.9999786 и ещё пять (одно действительное и две пары комплексных) с модулем менее 0.12.
При возведении в степень 200 только первые два будут иметь сколько-нибудь значимую величину.
1 соответствует тому, что сумма вероятностей сохраняется (всегда равна 1).
0.9999786 близко к , но оно немного отличается.
Все эти собственные значения являются точными корнями полинома .
Если туда подставить , то будет маленькое значение (примерно ), но не ноль.

zykov писал(а):Source of the post А при больших даёт правильную асимптотику.

Тут я немного погорячился. Асимптотика качественно правильная и даже довольно точная, но имеет небольшую ошибку.
Точная асимптотика: , где находится через собственные вектора.
А - это корень полинома чуть меньше 1 (примерно равен ).

Я даже не подозревала о таких глубинах в этой задаче. Я и четверти всего написанного не поняла с первого раза. Щас сижу, врубаюсь.
Спасибо всем. Если появятся вопросы, задам.

Элементарными методами эта задача не решается (только если приближенно).
Но как Ian заметил, это классический случай Марковских цепей.
Марковские процессы - это мощный инструмент. Обычно эту тему кратко затрагивают в конце курса по теорверу.

В данном случае можно рассмотреть конечный автомат с 7 состояниями, которому на вход подают последовтельность цифр (каждая от 1 до 6).
(В компьютерной области такое называют парсер, как например регулярные выражения в качестве частного случая парсера.)
Вначале автомат находится в состянии 1.
При получении нового входа он переходит из текущего состояния в новое (возможно тоже самое) в соответствии с таблицей (графом автомата).
Так из состояния 1 он переходит в состояние 2, если вход был "1". Иначе остается в состоянии 1.
Из состояния 2 переходит в состояние 3 при входе "2" или в состояние 2 (остается в нём) при входе "1". Иначе переходит в состояние 1.
Из 3 в 4 по входу "3", в 2 по входу "1", в 1 по остальным входам.
Аналогично для состояний 4 и 5.
Из состояния 6 переходит в 7 по входу "6", в 2 по входу "1", в 1 по любому другому входу.
Из состояния 7 всегда переходит обратно в 7 независимо от входа.

Переход в состояние 7 означает что автомат распознал последовательность "123456". После этого автомат остается в этом состоянии.
Таким образом, если автомат оказался в состянии 7 после 200 входов, значит где-то он встретил последовательность "123456" во время этих 200 входов. Если он оказался в любом другом состоянии, то такой последовательности не было.

Теперь рассмотрим вероятности.
Вначале автомат был в состоянии 1 с вероятность 100% процентов.
После первого входа он может перейти в состояние 2 с вероятность 1/6 или остатся в 1 с вероятностью 5/6.
Далее, если он был в состянии 1, будет тоже самое. Если он был в состоянии 2, то он может перейти в состоние 3 с вероятностью 1/6, остатся в 2 с вероятность 1/6 или перейти в 1 с вероятностью 4/6.
И так далее.

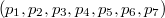
Вобщем если перед новым входом автомат имел распределение вероятностей по состониям (их сумма равна 1), то после получения нового входа (где все 6 вариантов имеют одинаковую вероятность, независимую от состояния автомата) вектор нового распределения вероятностей по состояниям автомата получается умножением строки-вектора старых вероятностей справа на матрицу, которую привел Ian.
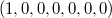
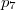
Если взять вектор и умножить его на эту матрицу 200 раз (или 1 раз на эту матрицу в степени 200), то получим вектор веротностей найти автомат в каждом из его 7 состояний после 200 входов. Вероятность - это вероятность того, что автомат где-то встретил последовательность "123456".

Меня тут спросили какие задачи можно предложить на олимпиаду топовым IT-студентам, чтобы не были решены в сети, я сразу подумал про эту. Но для этого она должна стать досчитываемой до точного ответа. Сделал дауншифт с 6 исходов до 3, типа корни уравнения 3й степени всегда есть явные.Но и там непросто
Задача. В алфавите три буквы А,В,С выбираемые с вероятностями [math]\alpha,\beta,\gamma. Рассматривается случайное слово длины N>2. Найти компактную формулу для вероятности, что в слове есть подслово АВС(7 баллов) Или хотя бы предложить линейный по N алгоритм вычисления этой вероятности (3 балла)

Решение для [math]\alpha=\beta=\gamma=\frac{1}{3}

Для n+1-го символа слова рассмотрим состояния после просмотра n символов: P - комбинации АВС еще не встречалось, последняя буква не А, последние 2 буквы не АВ; Q-комбинации АВС еще не встречалось, последняя буква А, R-комбинации АВС еще не встречалось, последние 2 буквы АВ, S -комбинация АВС встретилась среди предыдущих n букв. Это полная система непересекающихся гипотез. Обозначим их вероятности [math]p_{n},q_{n},r_{n},s_{n}.

По формулам полной вероятности[math]\begin{cases}
\begin{array}{ccccc}
p_{n+1}= & \frac{2}{3}p_{n} & +\frac{2}{3}q_{n} & +\frac{2}{3}r_{n}\\
q_{n+1}= & \frac{1}{3}p_{n}\\
r_{n+1}= & & \frac{1}{3}q_{n}\\
s_{n+1}= & & & \frac{1}{3}r_{n} & +s_{n}
\end{array}\end{cases}

При n=0 очевидно [math]p_{0}=1,q_{0}=r_{0}=s_{0}=0

Подстановкой сводим к одному рекуррентному уравнению [math]p_{n+1}=\frac{2}{3}(p_{n}+\frac{1}{3}p_{n-1}+\frac{1}{9}p_{n-2})

[math]p_{0}=1,p_{1}=\frac{2}{3},p_{2}=\frac{2}{3}

Любое [math]p_{n}=\lambda^{n}, где [math]\lambda^{3}=\frac{2}{3}(\lambda^{2}+\frac{1}{3}\lambda+\frac{1}{9})- корень кубического уравнения, автоматически удовлетворяет этому рекуррентному уравнению. И оно с данными 3-мя начальными условиями имеет единственное решение. Так как корней теоретически три, [math]\lambda_{1},\lambda_{2},\lambda_{3}, то [math]p_{n}=C_{1}\lambda_{1}^{n}+C_{2}\lambda_{2}^{n}+C_{3}\lambda_{3}^{n},где все С найдутся из подстановки n=0,1,2

По формуле Кардано https://studwork.org/spravochnik/matematika/reshenie-uravneniy-3-y-i-4-y-stepeni

[math]\lambda_{1}=\frac{2}{9}+\sqrt[3]{\frac{53}{729}+\frac{\sqrt{201}}{243}}+\sqrt[3]{\frac{53}{729}-\frac{\sqrt{201}}{243}}=0,973213

Разделив как-то с приближенными числами кубическое уравнение на [math]\lambda-\lambda_{1} , получим квадратное уравнение с комплексными корнями[math]\lambda_{2,3}=-0,15327\pm0,22939i

Естественно, действительные н.у и действительные коэффициенты гарантируют, что [math]C_{1}, будет действительно, а [math]C_{2},C_{3} комплексные, но такие, что действительным будет [math]p_{n}

Ответом задачи будет [math]s_{N}=1-p_{N}-q_{N}-r_{N}=1-p_{N}-\frac{1}{3}p_{N-1}-\frac{1}{9}p_{N-2}
Проблема: подобрать [math]\alpha,\beta,\gamma так, чтобы решение выразилось с помощью рациональных чисел, тогда ответ красив
Вторая попытка
Задача. В алфавите три буквы А,В,С выбираемые с вероятностями [math]\alpha,\beta,\gamma. Рассматривается случайное слово длины N>2. Найти компактную формулу для вероятности, что в слове есть подслово АВС(7 баллов)Найти линейный алгоритм нахождения этой вероятности (3 балла)

Решение

Для n+1-го символа слова рассмотрим состояния после просмотра n символов: P - комбинации АВС еще не встречалось, последняя буква не А, последние 2 буквы не АВ; Q-комбинации АВС еще не встречалось, последняя буква А, R-комбинации АВС еще не встречалось, последние 2 буквы АВ, S -комбинация АВС встретилась среди предыдущих n букв. Это полная система непересекающихся гипотез. Обозначим их вероятности [math]p_{n},q_{n},r_{n},s_{n}.

По формулам полной вероятности[math]\begin{cases}
\begin{array}{ccccc}
p_{n+1}= & (1-\alpha)p_{n} & +(1-\beta)q_{n} & +(\alpha+\beta)r_{n}\\
q_{n+1}= & \alpha p_{n}\\
r_{n+1}= & & \beta q_{n}\\
s_{n+1}= & & & (1-\alpha-\beta)r_{n} & +s_{n}
\end{array}\end{cases}

При n=0 очевидно [math]p_{0}=1,q_{0}=r_{0}=s_{0}=0

Подстановкой сводим к одному рекуррентному уравнению[math]p_{n+1}=(1-\alpha)p_{n}+(1-\beta)\alpha p_{n-1}+(\alpha+\beta)\alpha\beta p_{n-2}

[math]p_{0}=1,\quad p_{1}=1-\alpha,\quad p_{2}=(1-\alpha)^{2}+(1-\beta)\alpha

Это и есть почти полный алгоритм (см в конце)Продолжаем искать компактную формулу

Любое [math]p_{n}=\lambda^{n}, где [math]\lambda^{3}=(1-\alpha)\lambda^{2}+(1-\beta)\alpha\lambda+(\alpha+\beta)\alpha\beta- корень кубического уравнения, автоматически удовлетворяет этому рекуррентному уравнению. И оно с данными 3-мя начальными условиями имеет единственное решение. Так как корней теоретически три, [math]\lambda_{1},\lambda_{2},\lambda_{3}, то [math]p_{n}=C_{1}\lambda_{1}^{n}+C_{2}\lambda_{2}^{n}+C_{3}\lambda_{3}^{n},где все С найдутся из подстановки n=0,1,2

Решаем кубическое уравнение по методу Кардано. Сначала вводим [math]u=\lambda-\frac{1-\alpha}{3}

Получаем (*)[math]u^{3}+u\left[-\frac{(1-\alpha)^{2}}{3}-(1-\beta)\alpha\right]+\left[-\frac{2(1-\alpha)^{3}}{27}-\frac{\alpha(1-\alpha)(1-\beta)}{3}-\alpha\beta(\alpha+\beta)\right]=u^{3}+pu+q=0

Используем обозначение (**)[math]D=\left(\frac{p}{3}\right)^{3}+\left(\frac{q}{2}\right)^{2}=
[math]=-\frac{\alpha^{3}(1-\beta)^{3}}{27}-\frac{1}{108}\alpha^{2}(1-\beta)^{2}(1-\alpha)^{2}+\frac{\alpha^{2}\beta^{2}(\alpha+\beta)^{2}}{4}+\frac{\alpha^{2}(1-\alpha)\beta(1-\beta)(\alpha+\beta)}{6}+\frac{(1-\alpha)^{3}}{27}\alpha\beta(\alpha+\beta)
Формула Кардано [math]u_{1}=\sqrt[3]{-\frac{q}{2}+\sqrt{D}}+\sqrt[3]{-\frac{q}{2}-\sqrt{D}}
Иррациональность корня исчезает, когда можно представить[math]-\frac{q}{2}\pm\sqrt{D}=\left(g\pm h\sqrt{D}\right)^{3}, где [math]g,h рациональны
[math]\begin{cases}
\begin{array}{ccc}
-\frac{q}{2}=g^{3}+3gh^{2}D\\
(3g^{2}h+h^{3}D)\sqrt{D}=\sqrt{D}
\end{array}\end{cases}
....

Получим корень [math]\lambda=\frac{1-\alpha}{3}+2g

Ответом задачи будет [math]s_{N}=1-p_{N}-q_{N}-r_{N}=1-p_{N}-\frac{1}{3}p_{N-1}-\frac{1}{9}p_{N-2}

(это кстати и окончание алгоритма)

Ian писал(а):Source of the post Найти линейный алгоритм нахождения этой вероятности

Если под линейным алгоритмом имелось ввиду возведение матрицы в степень, то там всё намного проще.
Например , и т.д.
Учитывая, что , то нужно всего 9 умножений матриц - 3 возведения в квадрат и два раза возведение в 5 степень (на каждое по 3 умножения - 2 раза возведение в квадрат и ещё одно умножение на исходную матрицу).

Ian писал(а):Source of the post какие задачи можно предложить на олимпиаду топовым IT-студентам

Мне кажется, что это типовая задача на цепи Маркова. А типовая задача не очень подходит для олимпиады.
Если же студенты не изучали цепи Маркова, то предлагать им изобрести их - как-то жестко...

zykov писал(а):

Ian писал(а):Source of the post Найти линейный алгоритм нахождения этой вероятности

Если под линейным алгоритмом имелось ввиду возведение матрицы в степень, то там всё намного проще.

Нет конечно линейный значит рекуррентный расчет, число операций линейно по N.
То что Вы говорите может быть реализовано за число операций логарифмическое по N. Хоть нахождение степени матрицы, хоть степеней характеристических корней. А полный перебор экспоненциальный конечно. И я подумал что именно так вопросы поставить интересно, нашел линейный (рекуррентное уравнение) получил 3 балла, нашел формулу (и возможность найти ответ за C*lnN) получил еще 7.
По формулировке - задача должна входить в 100 самых фундаментальных задач теории вероятностей, быть во всех учебниках, а почему в России еще не вошла - потому что не все знают решение. В "Конкретной математике", гл. 8.4, учат получать компактный вид производящих функций чисел [math]p_N,\; F(z)=\sum p_N z^N, но именно эту задачу- не разбирают.
Но кто прочел главу- конечно решит и эту.