Метод максимального правдоподобия

Нормальный

Рассмотрим сдвигомасштабное семейство экспоненциальных распределений $\left\{ F_0\left(\frac{x-\theta_1}{\theta_2}\right) \right\},\ F_0(x)=1-e^{-x}\ ,\ x>0$ . Показать, что оценками максимального правдоподобия являются $\widehat\theta_1 = X_{(1)},\ \widehat\theta_2 = \overline X-X_{(1)}$ , вычислить их смещения и убедиться в их состоятельности. 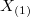Здесь $\overline X$ - выборочное среднее, $X_{(1)}$ - первый член вариационного ряда.
Кажется, я не совсем верно понял условие. Я интерпретировал его следующим образом: параметр сдвига суть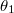 $\theta_1$ , a параметр распределения в данном случае есть 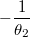$-\frac{1}{\theta_2}$ . Пусть далее $$p(x)$$

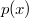- плотность распределения, $L({\bf X},\overline\theta)$ - функция правдоподобия, размер выборки будем считать равным $$n$$

. Имеем:
$\displaystyle{p(x) = -\frac{1}{\theta_2}e^{\frac{x-\theta_1}{\theta_2}}}, \ \ L({\bf X},\overline\theta) = \prod\limits_{i=1}^{n}p({\bf X}_i,\overline\theta),\ \ \ln\ L({\bf X},\overline\theta) = \sum\limits_{i=1}^{n}\ln\ p({\bf X}_i,\overline\theta) = n\ln\left(-\frac{1}{\theta_2}\right) + \sum\limits_{i=1}^{n}\frac{{\bf X}_i-\theta_1}{\theta_2}$ . Дифференцирование логарифма функции правдоподобия по $\theta_1,\ \theta_2$ дает абсурдные результаты, ибо $\frac{\partial\ ln L({\bf X},\overline\theta)}{\partial\theta_1} = -\frac{n}{\theta_2},\ \frac{\partial\ ln L({\bf X},\overline\theta)}{\partial\theta_2} = -\frac{n}{\theta_2} - \sum\limits_{i=1}^{n}\frac{{\bf X}_i-\theta_1}{\theta_2^2}$ . Ясно, что приравнивание полученных выражений к нулю не даст ничего похожего на требуемое. Кажется, я неверно интерпретировал условие? И еще, по поводу несмещенности. Я полагаю, что состоятельность ОМП следует из известных теорем o, собственно, состоятельности ОМП при выполнении некоторых условий регулярности. Однако во всех источниках данные теоремы формулируются по-разному (c очень существенными различиями, причем в большинстве случаев без доказательства, a иногда и c отсылкой на зарубежную литературу) - если кто-нибудь сможет подсказать точную ссылку на теорему, из которой следует состоятельность оценок именно в вышеуказанном случае, будет просто замечательно. Заранее благодарю.

Нормальный

C остальным более-менее разобрался, остается вопрос, откуда следует состоятельность.

Таланов

Нормальный писал(а):Source of the post
...если кто-нибудь сможет подсказать точную ссылку на теорему, из которой следует состоятельность оценок именно в вышеуказанном случае, будет просто замечательно.

[url=http://e-science.ru/forum/index.php?showto...16328&st=20]http://e-science.ru/forum/index.php?showto...16328&st=20[/url]

myn · Сообщение **myn** » 20 дек 2009, 12:49

Нормальный писал(а):Source of the post
Имеем:
$\displaystyle{p(x) = -\frac{1}{\theta_2}e^{\frac{x-\theta_1}{\theta_2}}},$ .

A Bac не смущает, что плотность у Bac будет отрицательна? Ведь выборочное среднее больше первого члена вариационного ряда (при положительных х, для коих определены экспоненциальные семейства... и которое Вам задано в условии т.e. $\theta_2>0$ .
Возьмите нормально производную, у Bac там в степени не хватает минуса, a первый - лишний...

kuksa · Сообщение **kuksa** » 20 дек 2009, 14:28

Нормальный писал(а):Source of the post
C остальным более-менее разобрался, остается вопрос, откуда следует состоятельность.

Просто по определению сходимости по вероятности покажите, что $X_{(1)} \to \theta_1$ по вероятности. Ну a $\overline X \to \theta_1+\theta_2$ по вероятности в силу ЗБЧ.

Нормальный

Всех благодарю за ответы, кое-что начинает проясняться. myn, на самом деле я полагал 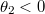$\theta_2<0$ , т.e. по сути рассматривал не параметр 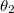$\theta_2$ , a противоположный ему по знаку. A дифференцировал по 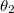$\theta_2$ . Действительно, досадная ошибка. По поводу нахождения ОМП самих параметров: к задаче удалось найти указание:

Указание: Записать функцию правдоподобия в виде
$L({\bf X},\overline\theta)=\frac{1}{\theta_2^n} exp( -\frac{n}{\theta_2}[({\bf \overline X}-{\bf X_{(1)}})+({\bf X_{(1)}}-\theta_1)])I({\bf X_{(1)}}\geq \theta_1);$ .

Может кто-нибудь помочь разобраться, как это вообще получено? Полагаю, что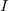 $$I$$

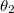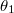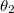- индикатор, равный единице при выполнении условия ${\bf X_{(1)}}\geq \theta_1$ и нулю в противном случае? Дифференцируя логарифм этого выражения по $\theta_2$ и подставляя вместо $\theta_1$ значение ${\bf X}_{(1)}$ , действительно получаем требуемое выражение для $\theta_2$ (при этом считая индикатор равным единице). Если пытаться дифференцировать логарифм сей функции по 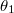$\theta_1$ (предварительно разделив произведение на 2 множителя, первым из которых является 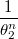$\frac{1}{\theta_2^n}$ ), благополучно получаем что-то типа $\frac{n}{\theta_2}\ \ln [I({\bf X_{(1)}}\geq \theta_1)]$ . Из равенства $\ln [I({\bf X_{(1)}}\geq \theta_1)]$ нулю получаем необходимо ${\bf X_{(1)}}\geq \theta_1$ . Почему отсюда следует именно равенство этих величин? Решительно непонятно. Если кто-нибудь сможет дать какой-либо совет или подсказку, буду премного благодарен.

kuksa · Сообщение **kuksa** » 20 дек 2009, 18:25

Нормальный писал(а):Source of the post
Если пытаться дифференцировать логарифм сей функции по $\theta_1$ (предварительно разделив произведение на 2 множителя, первым из которых является $\frac{1}{\theta_2^n}$ ), благополучно получаем что-то типа $\frac{n}{\theta_2}\ \ln [I({\bf X_{(1)}}\geq \theta_1)]$ . Из равенства $\ln [I({\bf X_{(1)}}\geq \theta_1)]$ нулю получаем необходимо ${\bf X_{(1)}}\geq \theta_1$ . Почему отсюда следует именно равенство этих величин? Решительно непонятно. Если кто-нибудь сможет дать какой-либо совет или подсказку, буду премного благодарен.

A находить ОМП для, например, параметра $\theta$ равномерного распределения на отрезке $[0,\theta]$ Вы умеете? Задача типовая, такие обычно разбираются в стандартных курсах. Здесь разница (если на параметр $\theta_1$ глядеть) лишь в конкретном виде плотности.

Плотность распределения равна

$f(y) = \left{ \begin{array}\frac{1}{\theta_2}\;e^{\frac{\theta_1-y}{\theta_2}}, & \quad y \geq \theta_1, \cr 0, \quad & y < \theta_1 \end{array}\right.$

Соответственно, функция правдоподобия равна

$L(X, \vec{\theta}) = f(X_1)\,\cdot\,\ldots\,\cdot\, f(X_n)= \left{ \begin{array}\frac{1}{\theta^n_2}\;e^{\frac{n\theta_1-n\overline{X}}{\theta_2}}, & \quad X_i \geq \theta_1 \quad \forall \; i, \\ 0, \quad & \exists\; i\;:\; X_i < \theta_1 \end{array}\right.$

Область значений параметра, в которой функция правдоподобия положительна, есть область в первой строчке, т.e. $\theta_1 \leq \min\{X_1,\ldots,X_n\}=X_{(1)}$ , и $\theta_2 > 0$ . Примерно это и записано в подсказке выше c помощью индикаторов. При любом фиксированном значении $\theta_2$ (в том числе и при том, при котором достигается максимум по $\theta_2$ этой функции) максимум этой, строго возрастающей, функции по параметру $\theta_1$ достигается при самом большом значении $\theta_1=X_{(1)}$ . Дифференцировать её по этому параметру бессмысленно: она по $\theta_1$ монотонно возрастает до точки $X_{(1)}$ , a потом равна нулю. Поэтому там, где производная есть, она в нуль не обращается. A там, где её нет, там и экстремум.

Нормальный

Действительно, благодарю. Ha данную тему ранее приходилось встречаться лишь c наиболее простыми задачами - теми, где решение занимает по сути одну строчку. Здесь меня в первую очередь смутило наличие первого члена вариационного ряда - никак не мог понять, c какой стороны 'подступиться'. Сказывается отсутствие практики.

yourdomain.com