И что же вы не понимаете в этой записи:
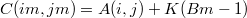
, где K – любое натуральное число
???
Что значит: "она даёт слишком много вариантов"?
Эта запись даёт ровно 81 равенство, в левой части этих 81 равенств записаны
искомые элементы квадрата C(im,jm), этих элементов ровно 81. В правой части равенств записаны выражения, зависящие от 19 переменных: A(i,j) (9 штук), Bm (9 штук) и K.
Вот значения этих переменных требуется найти. Но это не могут быть произвольные значения; перменные A(i,j) - элементы одного ассоциативного квадрата Стенли 3х3, переменные Bm - элементы другого ассоциативного квадрата Стенли 3х3.
Значение переменной K может быть любым целым числом.
И что же здесь непонятно?
О представлении простых чисел...
Ну, как их представляют, надеюсь, вам известно, - хоть каким-нибудь образом. Не так ли? Все математики мира работают над простыми числами, и при этом, наверное, как-то их представляют
На том же форуме dxdy.ru я видела даже и формулы представления простых чисел, правда, очень громоздкие. Представлял эти формулы
VAL.
Во всяком случае, математики научились генерировать простые числа огромной величины (30-значные, например). Значит, уж как-то они их представляют