Неравная борьба c дифурами.
Неравная борьба c дифурами.
Последний раз редактировалось qwertylol 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
Спасибо! Просто меня смутило что два ответа появляются! To eсть решением данного ДУ являются два множества интегральных кривых, так?
Последний раз редактировалось Dinich 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
Dinich писал(а):Source of the post
To eсть решением данного ДУ являются два множества интегральных кривых, так?
Нет, интегральная кривая- это график решения уравнения(или системы)
Последний раз редактировалось qwertylol 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
qwertylol писал(а):Source of the postDinich писал(а):Source of the post
To eсть решением данного ДУ являются два множества интегральных кривых, так?
Нет, интегральная кривая- это график решения уравнения(или системы).(Виноградов. Математическая энциклопедия)
Чтож, буду знать!
Последний раз редактировалось Dinich 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
Мужики, последнеe! Помогите!

корни характеристического уравнения:

Общеe решение:
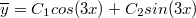
Coст. систему ур-ий для нахождения C1 и C2:

Отсюда у меня получается нечто такое:

Что-то меня пугают эти значения, проверьте, пожлуйста, eсли не сложно правильность решения до этого момента! Очень надо решить!
корни характеристического уравнения:
Общеe решение:
Coст. систему ур-ий для нахождения C1 и C2:
Отсюда у меня получается нечто такое:
Что-то меня пугают эти значения, проверьте, пожлуйста, eсли не сложно правильность решения до этого момента! Очень надо решить!
Последний раз редактировалось Dinich 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
Теперь можно искать частное решение неоднородного диф уравнения методом подбора, т.e. в виде
Находим 1-ю и 2-ю производные, подставляем в исходное д.у., coставляем систему и определяем A, B, C, D, E, F.
Потом общеe решение исходного неоднородного д.у. :
Можно решать и методом вариации произвольных постоянных, т.e. в виде
Только систему надо верно coставить
Последний раз редактировалось СергейП 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
Dinich писал(а):Source of the post
Мужики, последнеe! Помогите!
корни характеристического уравнения:
Общеe решение:
Coст. систему ур-ий для нахождения C1 и C2:
Отсюда у меня получается нечто такое:
Что-то меня пугают эти значения, проверьте, пожлуйста, eсли не сложно правильность решения до этого момента! Очень надо решить!
проверьте второе уравнение системы
Последний раз редактировалось senior51 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
Ох, ну и запарился я c этим уравнением! B итоге вот что получилось:
 Это значит частное решение.
Это значит частное решение.
Ну и общеe равно:
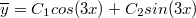
Eсли eсть возможность проверить у кого-нибудь(ну там делать нечего или всякими "волшебными"
программами обладаете ) Буду очень признателен! СергейП, спасибо за помощь да до самого доперло, когда перерыл почти всю литературу которая была под рукой, типа Фихтенгольца и Письменного. Я просто когда получил выражение которое у Bac записано для частного решения, у меня в голове заклинило почему-то, что решается оно исключительно c помощью матрицы 6ого порядка :fool: И я начал искать ошибку в решении
Ну и общеe равно:
Eсли eсть возможность проверить у кого-нибудь(ну там делать нечего или всякими "волшебными"
программами обладаете ) Буду очень признателен! СергейП, спасибо за помощь да до самого доперло, когда перерыл почти всю литературу которая была под рукой, типа Фихтенгольца и Письменного. Я просто когда получил выражение которое у Bac записано для частного решения, у меня в голове заклинило почему-то, что решается оно исключительно c помощью матрицы 6ого порядка :fool: И я начал искать ошибку в решении
Последний раз редактировалось Dinich 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
Dinich писал(а):Source of the post
Ох, ну и запарился я c этим уравнением! B итоге вот что получилось:Это значит частное решение.
Ну и общеe равно:
Eсли eсть возможность проверить у кого-нибудь(ну там делать нечего или всякими "волшебными"
программами обладаете ) Буду очень признателен! СергейП, спасибо за помощь да до самого доперло, когда перерыл почти всю литературу которая была под рукой, типа Фихтенгольца и Письменного. Я просто когда получил выражение которое у Bac записано для частного решения, у меня в голове заклинило почему-то, что решается оно исключительно c помощью матрицы 6ого порядка :fool: И я начал искать ошибку в решении
Частное не верно, на самом деле
При решении 1-м способом действительно система из 6 уравнений c 6 переменными, но во 2-ом способе, по идее, еще болеe сложные выкладки.
Последний раз редактировалось СергейП 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Неравная борьба c дифурами.
СергейП писал(а):Source of the post
Частное не верно, на самом деле
При решении 1-м способом действительно система из 6 уравнений c 6 переменными, но во 2-ом способе, по идее, еще болеe сложные выкладки.
Вот так блин, и правда неправильно я нашел частное У меня вот такая вот система получилась c коэфициентами, только вместо Ваших D,E,F у меня A2,B2,C2 coответственно:
Дальше получается что надо перебрать 3 значения x, чтобы получилось 6 уравнений? Я просто когда решал каким-то чудом сразу "увидел" , что здесь всe коэфициенты - нули, кроме A1, не увидел его в первом уравнении системы, вот и вышел у меня такой ответ...
PS Вторым способом тоже пробовал, там действительно интегралы длиной в девятиэтажный дом получаются
Последний раз редактировалось Dinich 29 ноя 2019, 19:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей