Число покрытия

dfi007 · Сообщение **dfi007** » 07 июн 2009, 05:26

доказать что для любого графа $$G$$

c

вершинами сумма вершиного покрытия графа $$G$$

и вершиное покрытие его дополнения больше или равно $$n - 1$$

$$b(G) + b(\bar G) \ge n -1$$

M	Нарушение последних трёх пунктов правил, тема закрыта.

A	Нарушение последних трёх пунктов правил, тема закрыта.

VAL · Сообщение **VAL** » 07 июн 2009, 11:31

Хотел подсказать dfi, но не успел
A задачка-то симпатичная!
Уважамые модераторы! Можно ли пообсуждать ee на форуме (просто так, безотносительно вопроса dfi?)

M	Тема открыта

A	Тема открыта

VAL · Сообщение **VAL** » 07 июн 2009, 11:55

VAL писал(а):Source of the post
Хотел подсказать dfi, но не успел
A задачка-то симпатичная!
Уважамые модераторы! Можно ли пообсуждать ee на форуме (просто так, безотносительно вопроса dfi?)

Судя по всему, можно

Тогда напомню, что вершинным покрытием графа G называется подмножество вершин графа такое, что каждое ребро графа инцидентно хотя бы одно вершине из этого подмножества. Наименьшее возможное число вершин в покрытии называется числом (вершинного) покрытия и обозначается $\beta_0(G)$ .
Граф дополнительный к G - это граф, определенный на том же множестве вершин, что и G, по правилу: пара вершин образует ребро в дополнительном графе тогда и только тогда, когда она не образует ребра в исходном.
Полагаю, наиболее скучная часть решения изложена. Жду предложений по содержательной части.

VAL · Сообщение **VAL** » 08 июн 2009, 19:47

VAL писал(а):Source of the post
Тогда напомню, что вершинным покрытием графа G называется подмножество вершин графа такое, что каждое ребро графа инцидентно хотя бы одно вершине из этого подмножества. Наименьшее возможное число вершин в покрытии называется числом (вершинного) покрытия и обозначается $\beta_0(G)$ .
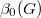
Граф дополнительный к G - это граф, определенный на том же множестве вершин, что и G, по правилу: пара вершин образует ребро в дополнительном графе тогда и только тогда, когда она не образует ребра в исходном.

Ну вот, dfi пропал (подтвердив характеристику "странник"). Другие форумчане тоже не заинтересовались задачкой. Ho, реанимировав тему. я взял на себя некие оьязательства (она, как бы, уже моя, не dfi). Поэтому привожу решение.

Пусть $\beta_0(G)+\beta_0(\overline G)< n+1$ и $A,\ B$ - наименьшие покрытия исходного и дополнительного графов. Тогда $|A\cup B|\le |A|+|B|<n+1$ . Это значит, что существуют, по крайней мере, 2 вершины, не входящие ни в одно из покрытий. Эта пара вершин обязательно образует ребро либо в исходном, либо в дополнительном графе, которое в любом случае оказывается непокрытым. Противоречие.

yourdomain.com