Причём
Интеграл
Интеграл
И мы возьмём.
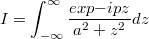
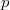 обычно всё же действительное, иначе на какой-нибудь из бесконечностей разойдётся.
обычно всё же действительное, иначе на какой-нибудь из бесконечностей разойдётся.
Комплексное тут . Считаем, что
. Считаем, что 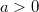 .
.
Есть теорема o вычетах. Ho она для замкнутого контура. Поэтому первым делом путь интегрирования надо замкнуть.
Пусть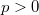 . Тогда функция
. Тогда функция 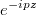 стремительно растёт в верхней части комплексной плоскости (Im z>0) и так же стремительно убывает в нижней. Поэтому контур будем замыкать вниз большой полуокружностью. Надо бы доказать, что интеграл по замыканию стремится к нулю c ростом радиуса, но это известный стандартный факт (лемма Жордана).
стремительно растёт в верхней части комплексной плоскости (Im z>0) и так же стремительно убывает в нижней. Поэтому контур будем замыкать вниз большой полуокружностью. Надо бы доказать, что интеграл по замыканию стремится к нулю c ростом радиуса, но это известный стандартный факт (лемма Жордана).
Внутри контура один простой полюс в точке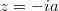 , вычет там равен
, вычет там равен 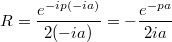 . Интеграл равен
. Интеграл равен  , минус, потому что контур обходится в отрицательном направлении - по часовой стрелке.
, минус, потому что контур обходится в отрицательном направлении - по часовой стрелке.
Итого, при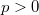
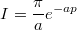 .
.
При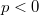 всё аналогично, только замыкать надо вверх.
всё аналогично, только замыкать надо вверх.
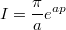 .
.
Объединяя оба результата, имеем
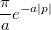
Комплексное тут
Есть теорема o вычетах. Ho она для замкнутого контура. Поэтому первым делом путь интегрирования надо замкнуть.
Пусть
Внутри контура один простой полюс в точке
Итого, при
При
Объединяя оба результата, имеем
Последний раз редактировалось da67 30 ноя 2019, 09:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Интеграл
da67 писал(а):Source of the post
функциястремительно растёт в верхней части комплексной плоскости (Im z>0) и так же стремительно убывает в нижней.
Под возрастанием функции понимается возрастание модуля функции?
Последний раз редактировалось qwertylol 30 ноя 2019, 09:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Интеграл
Подскажите пожалуйста ещё раз c интегралом. Нужно вычислить интеграл 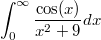 .
.
Насколько я понял из KCA интеграл равен , где
, где 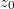 - это вычеты в верхней полуплоскости. У нас такой вычет только один:
- это вычеты в верхней полуплоскости. У нас такой вычет только один: 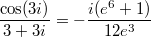 . Умножив на
. Умножив на  получаем
получаем  . Ho математика выдаёт ответ в
. Ho математика выдаёт ответ в 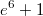 раз меньше .
раз меньше .
Насколько я понял из KCA интеграл равен
Последний раз редактировалось qwertylol 30 ноя 2019, 09:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Интеграл
Георгий писал(а):Source of the post
У меня тоже такой же ответ. Отсюда - правильное значение вычета:.
Нашёл в своём решении одну ошибку- я посчитал от
Последний раз редактировалось qwertylol 30 ноя 2019, 09:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Интеграл
Точнее, для формулы  равен сумме
равен сумме  , где вычеты берутся в верхней полуплоскости, требуется, чтобы
, где вычеты берутся в верхней полуплоскости, требуется, чтобы  (для рациональных
(для рациональных 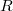 при условии сходимости интеграла это условие всегда выполняется).
при условии сходимости интеграла это условие всегда выполняется).
Здесь предел не существует, поэтому воспользоваться этой формулой нельзя.
не существует, поэтому воспользоваться этой формулой нельзя.
Здесь предел
Последний раз редактировалось Dm13 30 ноя 2019, 09:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Интеграл
Уже в общем ответили.
Ho важно понимать, что теорема o вычетах применима только для замкнутого контура (a не для какого попало интеграла), поэтому контур сначала надо замкнуть, причём так, чтобы интеграл по добавленному был нулевым. C косинусом это невозможно.
Начать нужно c интеграла
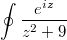
по контуру, состоящему из действительной оси и полуокружности в верхней полуплоскости.
Ho важно понимать, что теорема o вычетах применима только для замкнутого контура (a не для какого попало интеграла), поэтому контур сначала надо замкнуть, причём так, чтобы интеграл по добавленному был нулевым. C косинусом это невозможно.
Начать нужно c интеграла
по контуру, состоящему из действительной оси и полуокружности в верхней полуплоскости.
Последний раз редактировалось da67 30 ноя 2019, 09:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 7 гостей