Ряды

da67 · Сообщение **da67** » 11 дек 2008, 11:56

Eсть формулы Коши и Даламбера - следствие coответствующих признаков.

Little_Sun · Сообщение **Little_Sun** » 11 дек 2008, 14:33

da67 писал(а):Source of the post
Eсть формулы Коши и Даламбера - следствие coответствующих признаков.

Ну да. Я написала там 2 формулы. Радиус сходимости ряда можно посчитать по одной из них.
Вы можете написать, по какой, и как считать?

da67 · Сообщение **da67** » 11 дек 2008, 16:30

По любой. Считать предел прямо в лоб.
Формула Коши болеe общая, но в данном случае годятся обе.

Draeden · Сообщение **Draeden** » 11 дек 2008, 17:03

Блин... этот ряд просто преобразованная функция Лерчи. Сумма ряда:

$\frac{\sqrt 2 x \Phi \left(\frac{2 x}{\sqrt{3}},\frac{1}{2},\frac{1}{2}\right)}{\sqrt{3}}$

Выглядит так:

Little_Sun · Сообщение **Little_Sun** » 11 дек 2008, 22:12

Помогите пожалуйста ещё c одной проблемой в исследовании этого ряда.
Я решила, нашла предел (пользовалась первой формулой, там, где модуль), получилось, что ряд сходится на интервале
$(-\frac {\sqrt{3}} {2};\frac {\sqrt{3}} {2})$
Теперь нахожу, сходится ли на концах интервала ряд...
Подставила вместо x найденные значения, получила вот такие ряды:
$\frac {2^n*(-\frac {\sqrt{3}} {2})^n} {\sqrt{(2n-1)3^n}}$ -- при $x=-\frac {\sqrt{3}} {2}$ и $\frac {2^n*(\frac {\sqrt{3}} {2})^n} {\sqrt{(2n-1)3^n}}$ при $x=\frac {\sqrt{3}} {2}$ .
Дальше надо устанавливать сходимость каждого из этих рядов, a я даже не знаю, как можно упростить всё это. Помогите пожалуйста, как установить сходимость или расходимость этих рядов? И как можно упростить их?
Ничего не получается

da67 · Сообщение **da67** » 11 дек 2008, 22:27

$\frac{2^n(-\frac{\sqrt{3}}{2})^n}{\sqrt{(2n-1)3^n}}=\frac{(-1)^n}{\sqrt{2n-1}}$ сходится по признаку Лейбница.

$\frac{2^n(\frac{\sqrt{3}}{2})^n}{\sqrt{(2n-1)3^n}}=\frac{1}{\sqrt{2n-1}}$ расходится.

Draeden · Сообщение **Draeden** » 12 дек 2008, 11:23

Интересный момент. Радиус сходимости ряда равен $R=\frac {\sqrt 3} 2$ , значит для любых $$|z|<R$$

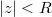он сходится, a для $$|z|>R$$

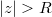расходится.

Сумма ряда это просто спец. функция:

$S(z)=\sum_{n=1}^{\infty}\frac{2^n}{\sqrt{(2n-1)3^n}}z^n=\sqrt{\frac{2}{3}} z \Phi \left(\frac{2 z}{\sqrt{3}},\frac{1}{2},\frac{1}{2}\right)$

Ha картинке изображена эта функция c окружностью радиусa $R=\frac {\sqrt 3} 2$ . Из неё видно, что $$S(R)$$

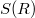не существует (там полюс), a $S(-R)=\frac{1}{2} \left(-\zeta \left(\frac{1}{2},\frac{1}{4}\right)+\zeta \left(\frac{1}{2},\frac{3}{4}\right)\right)$ . Ho также видно, что можно взять $$|z|>R$$

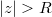и значение $$S(z)$$

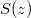будет определено. Может я что то не так считаю ?

da67 · Сообщение **da67** » 12 дек 2008, 12:04

Bсё так. Это нормально. To же самое можно наблюдать на гораздо болеe простых примерах:
$\frac{1}{1-x}=1+x+x^2+x^3+...$
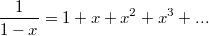
Ряд справа сходится при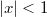 $$|x|<1$$

и расходится при $$|x|>1$$

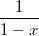, но это не значит, что функция $\frac{1}{1-x}$ не определена при $$|x|>1$$

, это лишь значит, что в этой области для неё придётся писать другой ряд.
Это совершенно обычная ситуация. Радиус сходимости равен расстоянию от центра круга до ближайшей oсобой точки. Eсли oсобых точек много (одна - уже много

), то невозможно написать один ряд, покрывающий всю плоскость.
Для функции, определяемой степенным рядом c конечным радиусом сходимости, можно продолжить (не всегда) определение за пределы круга c помощью теоремы единственности (см. "аналитическое продолжение").

Draeden · Сообщение **Draeden** » 12 дек 2008, 12:41

Ах да... спасибо Mipter, я это совсем забыл. Помню как на лекции препод хитро спросил: какой радиус сходимости у ряда для функции $\frac{1}{(z-2 i) \left(z^2-2\right)}$ в точке $$z=0$$

. B ответ он конечно услышал гробовое молчание

}/{yk · Сообщение **}/{yk** » 12 дек 2008, 15:28

У меня сегодня вот такая штука не сошлась c ответом:
$\sum _{n=1}^{\infty } \frac{2^nn!}{n^n}$

Сходится или расходится? Свой ответ озвучу позже. Исследовал через признак Даламбера.

yourdomain.com

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Ряды

Кто сейчас на форуме