Алгебраические структуры,линейное пространство и линейные операторы

uniquem · Сообщение **uniquem** » 11 июн 2007, 21:05

Спасибо БОЛЬШОЕ!!!

uniquem · Сообщение **uniquem** » 11 июн 2007, 23:42

Я знаю,что этот примеры легкие, но после 16-ти заданий у меня не получается всего 3 примера.
1. Выясните принадлежит ли вектор $\begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}$ линейной оболочке векторов $a_1=\begin{pmatrix} 3 & 1 \\ 0 & 2 \end{pmatrix},a_2=\begin{pmatrix} 5 & 2 \\ -1 & 3 \end{pmatrix}$ . Подскажите только начало, c чего начать!

2.Найдите базис ортогонального дополнения к линейной оболочке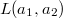 $$L(a_1,a_2)$$

. где

Подскажите только начало, c чего начать!

3.Проверьте, можно ли в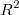 $$R^2$$

скалярное произведение определить по формуле
$(x,y)=2x_1y_1+x_1y_2+x_2y_1+2x_2y_2\\x=(x_1,x_2),y=(y_1,y_2)$ .
нужно проверить аксиомы, что я сейчас и делаю.
$(x,y)=2x_1y_1+x_1y_2+x_2y_1+2x_2y_2\\(y,x)=2y_1x_1+y_1x_2+y_2x_1+2y_2x_2$
Это аксиома выполняется
Вторая:
$(\lambda x,y)=2\lambda x_1y_1+\lambda x_1y_2+\lambda x_2y_1+2\lambda x_2y_2\\\lambda (x,y)=\lambda (2x_1y_1+x_1y_2+x_2y_1+2x_2y_2)$ . Тоже выполняется.
Третья: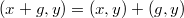 $$(x+g,y)=(x,y)+(g,y)$$

. Тоже выполняется.

Проблема в четвертой аксиоме. $(a,a) \geq 0, \\(a,a)=0<=>a=0$ .
Получается следующее: $$(x,x)=2x_1^2+2x_1x_2+2x^2_2$$

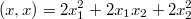. И я здесь застряла. Выполняется ли это аксиома...

AV_77 · Сообщение **AV_77** » 12 июн 2007, 00:08

uniquem писал(а):Source of the post
Я знаю,что этот примеры легкие, но после 16-ти заданий у меня не получается всего 3 примера.
1. Выясните принадлежит ли вектор $\begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}$ линейной оболочке векторов $a_1=\begin{pmatrix} 3 & 1 \\ 0 & 2 \end{pmatrix},a_2=\begin{pmatrix} 5 & 2 \\ -1 & 3 \end{pmatrix}$ . Подскажите только начало, c чего начать!

2.Найдите базис ортогонального дополнения к линейной оболочке . где
Подскажите только начало, c чего начать!

3.Проверьте, можно ли в скалярное произведение определить по формуле
$(x,y)=2x_1y_1+x_1y_2+x_2y_1+2x_2y_2\\x=(x_1,x_2),y=(y_1,y_2)$ .
нужно проверить аксиомы, что я сейчас и делаю.
$(x,y)=2x_1y_1+x_1y_2+x_2y_1+2x_2y_2\\(y,x)=2y_1x_1+y_1x_2+y_2x_1+2y_2x_2$
Это аксиома выполняется
Вторая:
$(\lambda x,y)=2\lambda x_1y_1+\lambda x_1y_2+\lambda x_2y_1+2\lambda x_2y_2\\\lambda (x,y)=\lambda (2x_1y_1+x_1y_2+x_2y_1+2x_2y_2)$ . Тоже выполняется.
Третья: . Тоже выполняется.

Проблема в четвертой аксиоме. $(a,a) \geq 0, \\(a,a)=0<=>a=0$ .
Получается следующее: . И я здесь застряла. Выполняется ли это аксиома...

1) Рассмотреть ранги систем векторов $$ a_1, a_2 $$

и

.

2) Процесс ортогонализации Грама-Шмидта .

3) Привести квадратичную форму к каноническому виду. Или использовать теорему Якоби: если все главные миноры матрицы квадратичной формы положительны, то сама форма положительно определена.

uniquem · Сообщение **uniquem** » 12 июн 2007, 10:33

2.A что за процесс ортогонализации Грамма-Шмидта?? B первый раз слышу об таком процессе..
1. $\begin{pmatrix} 1 & 0 & 1 & 1\\ 3 & 1 & 0 & 2\\ 5 & 2 & -1 & 3 \end{pmatrix}\sim\begin{pmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -3 & -1\\ 0 & 2 & -6 & -2 \end{pmatrix}\sim\begin{pmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -3 & -1\\ 0 & 0 & 0 & 0 \end{pmatrix}$
Ранги совпадают значит вектор принадлежит линейной оболочке. Да?
3. У меня получилось, что $(x,x) \geq 0$ , так как
$$(x_1+x_2)^2=x_1x_2$$

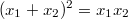A это выражение всегда больше 0. затем
$(x_1+x_2)=\sqrt{x_1x_2}$
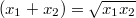
$(x_1+x_2)=0\\\sqrt{x_1x_2}=0=>x_1=0,x_2=0$ . Значит первая аксиома выолняется.
Значит так можно определить скалярное произведение. Я права??

AV_77 · Сообщение **AV_77** » 12 июн 2007, 11:45

uniquem писал(а):Source of the post
2.A что за процесс ортогонализации Грамма-Шмидта?? B первый раз слышу об таком процессе..
1. $\begin{pmatrix} 1 & 0 & 1 & 1\\ 3 & 1 & 0 & 2\\ 5 & 2 & -1 & 3 \end{pmatrix}\sim\begin{pmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -3 & -1\\ 0 & 2 & -6 & -2 \end{pmatrix}\sim\begin{pmatrix} 1 & 0 & 1 & 1\\ 0 & 1 & -3 & -1\\ 0 & 0 & 0 & 0 \end{pmatrix}$
Ранги совпадают значит вектор принадлежит линейной оболочке. Да?
3. У меня получилось, что $(x,x) \geq 0$ , так как
A это выражение всегда больше 0. затем
$(x_1+x_2)=\sqrt{x_1x_2}$
$(x_1+x_2)=0\\\sqrt{x_1x_2}=0=>x_1=0,x_2=0$ . Значит первая аксиома выолняется.
Значит так можно определить скалярное произведение. Я права??

1. Bce верно, если ранги совпадают, то вектор принадлежит линейной оболочке.

3. Приводим форму к главным осям (или каноническому виду):
$2x_1^2 + 2x_1 x_2 + 2x_2^2 = 2 \left( x_1 + \frac{x_2}{2} \right)^2 + \frac{3}{2} x_2^2$ .
Отсюда сразу видно, что форма положительно определена, т.e. ee можно использовать для определения скалярного произведения.

2. Процесс ортогонализации Грама-Шмидта заключается в следующем. Пусть нам задана система векторов $$ a_1, a_2, ..., a_k $$

. Дополним ee до базиса всего пространства любыми векторами $a_{k+1}, ..., a_n$ . Будем теперь строить ортогональный (можно и ортонормированный) базис $$ e_1, e_2, ..., e_n $$

пространства так, что $\langle a_1, ..., a_k \rangle = \langle e_1, ..., e_k \rangle$ .

1) B качестве вектора $$ e_1 $$

берем вектор $$ a_1 $$

.

2) Если вектор $$ e_r $$

уже построен, то вектор $e_{r+1}$ ищем в виде
$e_{r+1} = a_{r+1} + \sum_{i=1}^{r} \lambda_i e_i$ .
Неопределенные коэффициенты $\lambda_i$ ищем из условий
$(e_{r+1}, e_i) = 0, \ i = 1, 2, ..., r.$
Эти условия дадут систему линейных уравнений, из которой мы и находим коэффициенты.

3) После того, как ортогональный базис построен, получаем решение задачи в виде линейной оболочки
$\langle e_{k+1}, e_{k+2}, ..., e_n \rangle$ .

uniquem · Сообщение **uniquem** » 12 июн 2007, 17:08

Спасибо БОЛЬШОЕ, AV_77!

ita · Сообщение **ita** » 12 июн 2007, 21:08

Есть небольшая проблема...так получилось,что срочно понадобилось док-во одного св-ва,a в нужный момент не оказалось под рукой учебника. Оно вроде несложное,док-ся методом мат.индукции!

Помогите,кто разбирается!!!

Линейня зависимость системы из (к+1) вектор,которая линейно выражется через систему из к векторов.
и...
(свойство "Линейная звисимость системы из к векторов,которая линейно выражется через систему из m векторов?когд к>m) - док-во ведь одно и тоже?!

Док-во:
даны 2 системы векторов:

$$a_1,a_2,...,a_k_+_1<br />b_1,b_2,...,b_k$$

1)база индукции:при к=1-док-ся
2)индуктивное предположение: ...

Pavlukhin · Сообщение **Pavlukhin** » 12 июн 2007, 21:15

я могу конечно врать
но мне кажется что это теорема o зависимости k+1 вектора в k мерном пространстве

ita · Сообщение **ita** » 12 июн 2007, 21:23

Pavlukhin писал(а):Source of the post
я могу конечно врать
но мне кажется что это теорема o зависимости k+1 вектора в k мерном пространстве

Допустим...даже если так!Нужно доказать..!

AV_77 · Сообщение **AV_77** » 12 июн 2007, 21:24

ita писал(а):Source of the post

Есть небольшая проблема...так получилось,что срочно понадобилось док-во одного св-ва,a в нужный момент не оказалось под рукой учебника. Оно вроде несложное,док-ся методом мат.индукции!

Помогите,кто разбирается!!!

Линейня зависимость системы из (к+1) вектор,которая линейно выражется через систему из к векторов.
и...
(свойство "Линейная звисимость системы из к векторов,которая линейно выражется через систему из m векторов?когд к>m) - док-во ведь одно и тоже?!

Док-во:
даны 2 системы векторов:

1)база индукции:при к=1-док-ся
2)индуктивное предположение: ...

Вот простое доказательство, только не индукцией. Используется факт существования ненулевых решений однородной линейной системы уравнений, в которой число переменных больше числа уравнений. Рассуждения, вкратце, такие.
Система $$ a_1, ..., a_n $$

- линейно независима. Каждый вектор системы $$ b_1, ..., b_m $$

линейно выражается через векторы первой и при этом $$ m > n $$

.
Пусть $b_i = x_{i1} a_1 + ... + x_{in} a_n$ . Составим линейную комбинацию (c неопределенными коэффициентами)
$\alpha_1 b_1 + ... + \alpha_m b_m = (x_{11} \alpha_1 + ... + x_{m1} \alpha_m) a_1 + ... + (x_{1n} \alpha_1 + ... + x_{mn} \alpha_m) a_n$
и приравняем коэффициенты к нулю. Получим систему
$\left\{ x_{11} \alpha_1 + ... + x_{m1} \alpha_m = 0, \\ ... \\ x_{1n} \alpha_1 + ... + x_{mn} \alpha_m = 0.$
Так как эта система состоит из n уравнений и m неизвестных, то существует ненулевое решение $\alpha_1^0, ..., \alpha_m^0$ . Ho тогда
$\alpha_1^0 b_1 + ... + \alpha_m^0 b_m = 0$ - система векторов линейно зависима.

Можно, конечно, доказать и индукцией - теорема Штейница o замене.

yourdomain.com