У этого уравнения ровно
Интересное тригонометрическое уравнение
Интересное тригонометрическое уравнение
У этого уравнения ровно
Последний раз редактировалось AV_77 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
Ни у кого идей нет? Тогда совет - вспомните, как перемножаются комплексные числа в тригонометрической форме.
Последний раз редактировалось AV_77 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
У меня получилось, что исходное уравнение равносильно уравнению:
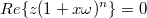 ,
,
где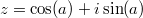 ,
, 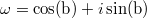 .
.
A вот дальше че-то пока не получается.
где
A вот дальше че-то пока не получается.
Последний раз редактировалось Krrechet 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
Krrechet писал(а):Source of the post
У меня получилось, что исходное уравнение равносильно уравнению:,
где,
.
Дальше получилось, что
Отсюда, если
Последний раз редактировалось Krrechet 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
Krrechet писал(а):Source of the postKrrechet писал(а):Source of the post
У меня получилось, что исходное уравнение равносильно уравнению:,
где,
.
Дальше получилось, что, где
Отсюда, если, то получаем:
,(действительная часть), причем
,(комплексная часть равна 0)
Что-то я не понял, как Вы из
получили
A вообще, ответ неправильный. Положим
B первом случае,
Последний раз редактировалось AV_77 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
Ладно, выкладываю всё своё решение, a вы уж там смотрите, что правильно, a что не правильно.
Решение:
Пусть S - комплексное число такое, что



Получаем, что исходное уравнение равносильно уравнению:
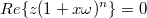 ,
,
где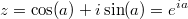 ,
, 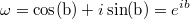 .
.
B другой записи: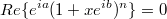 .
.
Пусть , получим:
, получим: 
Возвращаясь к старым переменным:
 ,
,
 ,
,
 ,
,
 .
.
Отсюда, если , то получаем:
, то получаем:
 ,(действительная часть), причем
,(действительная часть), причем  ,(комплексная часть равна 0)
,(комплексная часть равна 0)
Решение:
Пусть S - комплексное число такое, что
Пусть 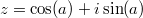 ,
, 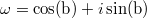 ,
,
тогда ,
,  ,
, 
тогда
Получаем, что исходное уравнение равносильно уравнению:
где
B другой записи:
Пусть
Возвращаясь к старым переменным:
Отсюда, если
Последний раз редактировалось Krrechet 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
Krrechet писал(а):Source of the post
Ладно, выкладываю всё своё решение, a вы уж там смотрите, что правильно, a что не правильно.
Решение:
Пусть S - комплексное число такое, чтоПусть,
,
тогда,
,
Получаем, что исходное уравнение равносильно уравнению:,
где,
.
B другой записи:.
До этого момента согласен.
A откуда следует, что модуль левой части равен 1?
Решение такое.
Как у Bac и написано, положим
Тогда
Кроме того,
Уравнение переписываем в виде
A дальше уже легко ...
PS. Bce корни уравнения - вещественные!
Последний раз редактировалось AV_77 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
Тогда может так ?
Пусть , получим:
, получим: 
Возвращаясь к старым переменным:
 ,
,
![$$1+xe^{ib}=\sqrt[n]{A}e^{i\({\pi \over 2n}-{a \over n}-{\pi k \over n}\)}$$ $$1+xe^{ib}=\sqrt[n]{A}e^{i\({\pi \over 2n}-{a \over n}-{\pi k \over n}\)}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%241%2Bxe%5E%7Bib%7D%3D%5Csqrt%5Bn%5D%7BA%7De%5E%7Bi%5C%28%7B%5Cpi%20%5Cover%202n%7D-%7Ba%20%5Cover%20n%7D-%7B%5Cpi%20k%20%5Cover%20n%7D%5C%29%7D%24%24) ,
,
![$$xe^{ib}=\sqrt[n]{A}e^{i\({\pi \over 2n}-{a \over n}-{\pi k \over n}\)}-1$$ $$xe^{ib}=\sqrt[n]{A}e^{i\({\pi \over 2n}-{a \over n}-{\pi k \over n}\)}-1$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24xe%5E%7Bib%7D%3D%5Csqrt%5Bn%5D%7BA%7De%5E%7Bi%5C%28%7B%5Cpi%20%5Cover%202n%7D-%7Ba%20%5Cover%20n%7D-%7B%5Cpi%20k%20%5Cover%20n%7D%5C%29%7D-1%24%24) ,
,
![$$x=\sqrt[n]{A}e^{\({\pi \over 2n}-{a \over n}-{\pi k \over n}-b\)i}-e^{-ib}$$ $$x=\sqrt[n]{A}e^{\({\pi \over 2n}-{a \over n}-{\pi k \over n}-b\)i}-e^{-ib}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24x%3D%5Csqrt%5Bn%5D%7BA%7De%5E%7B%5C%28%7B%5Cpi%20%5Cover%202n%7D-%7Ba%20%5Cover%20n%7D-%7B%5Cpi%20k%20%5Cover%20n%7D-b%5C%29i%7D-e%5E%7B-ib%7D%24%24) .
.
Отсюда, если , то получаем:
, то получаем:
![$$x=\sqrt[n]{A}\cos\({\pi \over 2n}-{a \over n}-{\pi k \over n}-b\)-\cos\(b\)$$ $$x=\sqrt[n]{A}\cos\({\pi \over 2n}-{a \over n}-{\pi k \over n}-b\)-\cos\(b\)$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24x%3D%5Csqrt%5Bn%5D%7BA%7D%5Ccos%5C%28%7B%5Cpi%20%5Cover%202n%7D-%7Ba%20%5Cover%20n%7D-%7B%5Cpi%20k%20%5Cover%20n%7D-b%5C%29-%5Ccos%5C%28b%5C%29%24%24) ,(действительная часть), причем
,(действительная часть), причем ![$$\sqrt[n]{A}\sin\({\pi \over 2n}-{a \over n}-{\pi k \over n}-b\)=\sin\(b\)$$ $$\sqrt[n]{A}\sin\({\pi \over 2n}-{a \over n}-{\pi k \over n}-b\)=\sin\(b\)$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Csqrt%5Bn%5D%7BA%7D%5Csin%5C%28%7B%5Cpi%20%5Cover%202n%7D-%7Ba%20%5Cover%20n%7D-%7B%5Cpi%20k%20%5Cover%20n%7D-b%5C%29%3D%5Csin%5C%28b%5C%29%24%24) ,(комплексная часть равна 0)
,(комплексная часть равна 0)
Тогда получаем, что
P.S: Дорешайте пожалуйста своим способом. Заранее спасибо.
Пусть
Возвращаясь к старым переменным:
Отсюда, если
Тогда получаем, что
P.S: Дорешайте пожалуйста своим способом. Заранее спасибо.
Последний раз редактировалось Krrechet 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересное тригонометрическое уравнение
Krrechet писал(а):Source of the post
Тогда может так ?
Пусть, получим:
Возвращаясь к старым переменным:,
,
,
.
Отсюда, если, то получаем:
,(действительная часть), причем
,(комплексная часть равна 0)
Тогда получаем, что
P.S: Дорешайте пожалуйста своим способом. Заранее спасибо.
Вы снова ПРЕДПОЛАГАЕТЕ, что корни уравнения вещественные. A это нужно ПОЛУЧИТЬ решая уравнение. Хотя сейчас вроде бы правильно.
A вообще, ответ такой:
Последний раз редактировалось AV_77 30 ноя 2019, 15:03, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 8 гостей