Центр масс системы материальных точек.

Anik · Сообщение **Anik** » 04 дек 2015, 12:23

Пусть задано взаимное расположение $$n$$

материальных точек системы, $n\geqslant 2$ . Проведём из какой-либо точки системы (например, $$m_1$$

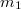
), радиус-векторы ко всем точкам системы, и рассмотрим их линейную комбинацию с коэффициентами, равными массам соответствующих точек. Условимся называть радиус-вектор материальной точки, умноженный на массу данной точки материализованным вектором точки, а точку, из которой проведён радиус-вектор, центром материализованного вектора. Таким образом, упомянутая линейная комбинация векторов представляет собой сумму материализованных векторов точек, проведённых из заданного центра. На Рис. этим центром является точка $$m_1$$

.
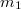
При неизменном взаимном расположении материальных точек, с изменением центра материализованных векторов, их сумма изменяется. Существует такой единственный центр в системе материальных точек, что сумма материализованных векторов для этого центра равна нулю. Этот центр называется центром масс системы материальных точек, и обозначается буквой $$C$$

.

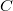
Если сумму масс всех точек системы обозначить за $$M$$

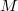
, то можно ввести такое определение:
Центром масс системы $$n$$

материальных точек

называется геометрическая точка

, для которой $\sum_{n}^{i=1}m_i\vec r_{ci}=0$ ,
Мы докажем следующую теорему: сумма материализованных векторов, проведённых из любой точки системы, делённая на сумму масс всех точек системы даёт радиус-вектор, указывающий на центр масс системы материальных точек.

zykov · Сообщение **zykov** » 04 дек 2015, 15:05

Это будет теоремой только если дадите альтернативное определение центра масс. А так это определение.
PS: вместо того, чтобы марать форум, лучше бы книжки почитали...

12d3 · Сообщение **12d3** » 04 дек 2015, 15:53

Anik писал(а):Source of the post Центром масс системы материальных точек называется геометрическая точка , для которой

Такое определение плохо тем, что надо доказывать существование такой точки. Чем вам обычное определение не нравится?

Anik · Сообщение **Anik** » 05 дек 2015, 05:40

$m_1\vec r_{11}+m_2\vec r_{12}+..+m_n\vec r_{1n}=m_1(\vec r_{1c}+\vec r_{c1})+m_2(\vec r_{1c}+\vec r_{c2})+..+m_n(\vec r_{1c}+\vec r_{cn})=(m_1+m_2+...+m_n)\vec r_{1c}+m_1\vec r_{c1}+m_2\vec r_{c2}+...+m_n\vec r_{cn}$
$\sum_{n}^{i=1}m_i\vec r_{1i}=M\vec r_{1c}+\sum_{n}^{i=1}m_i\vec r{ci}$
Учитывая, что последнее слагаемое по определеню центра масс равно нулю, имеем:
$M^{-1}\sum_{n}^{i=1}m_i\vec r_{1i}=\vec r_{1c}$
Что и требовалось доказать.
Т.е. сумма материализованных векторов, проведённых из произвольной точки системы к оставшимся точкам, делённая на массу всей системы, даёт вектор, указывающий на центр масс системы материальных точек.

Anik · Сообщение **Anik** » 05 дек 2015, 05:48

12d3 писал(а):Source of the post Такое определение плохо тем, что надо доказывать существование такой точки. Чем вам обычное определение не нравится?

Обычное определение центра масс не указыват на замечательную особенность центра масс, а именно, на нулевое значение суммы материализованных векторов, проведённых из центра масс. Обычное определение центра масс просто определяет некоторую точку, а что это за точка, в чём её смысл, - непонятно.
Можно ещё доказать, что существует единственная точка в системе материальных точек, обладающая такой особенностью.

Anik · Сообщение **Anik** » 05 дек 2015, 06:00

У меня в стартовом сообщении была ошибка, я её устранил.

individ.an · Сообщение **individ.an** » 05 дек 2015, 09:04

Вот дурдом!
Это, что выходит надо решать уравнения?
И какой в этом смысл? Не легче воспользоваться стандартным определением цетра массы системы и сразу получить ответ?

Anik · Сообщение **Anik** » 05 дек 2015, 10:13

individ.an писал(а):Source of the post Вот дурдом! Это, что выходит надо решать уравнения?

Никаких уравнений решать не надо. Центр масс находится по формуле : $M^{-1}\sum_{n}^{i=1}m_i\vec r_{1i}=\vec r_{1c}$
Здесь все векторы проведены из точки $$m_1$$

к остальным точкам системы, но можно взять в качестве начальной любую точку системы, например $$m_3$$

.
Тогда будет:
$M^{-1}\sum_{n}^{i=1}m_i\vec r_{3i}=\vec r_{3c}$

ALEX165 · Сообщение **ALEX165** » 05 дек 2015, 13:13

Anik писал(а):Source of the post Обычное определение центра масс не указыват на замечательную особенность центра масс, а именно, на нулевое значение суммы материализованных векторов, проведённых из центра масс.

Это Вам не указывает, а для остальных:
Достаточно в $\sum m_i \vec r_i=( \sum m_i)\vec R$ положить $\vec R=\vec 0$

Anik · Сообщение **Anik** » 05 дек 2015, 13:51

ALEX165 писал(а):Source of the post
Anik писал(а):Source of the post

Обычное определение центра масс не указыват на замечательную особенность центра масс, а именно, на нулевое значение суммы материализованных векторов, проведённых из центра масс.

Это Вам не указывает, а для остальных:
Достаточно в $\sum m_i \vec r_i=( \sum m_i)\vec R$ положить $\vec R=\vec 0$

Достаточно в $\sum m_i \vec r_i=( \sum \vec r _i) M$ положить $$M=0$$

Ну и что?

yourdomain.com