Здравствуйте!
Необходимо показать, что функция
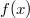
возрастает если

возрастает по абсолютному значению. Найти производную трудновато, потому что функция очень громоздкая и зависит от большого числа параметров. Однако, получилось показать, что

больше чем
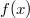
. Отсюда вывод, что функция возрастает если

возрастает по абсолютному значению. Скажите ничего ли не упущено, всё-ли правильно?
Спасибо.
Последний раз редактировалось
Math 27 ноя 2019, 19:28, всего редактировалось 1 раз.
Причина: test