Индекс комплексного векторного поля
- Dr. Arrieta
- Сообщений: 458
- Зарегистрирован: 02 авг 2009, 21:00
Индекс комплексного векторного поля
Все равно не понимаю...Например точка 4. Почему же мы не рисуем этот вектор между двумя вами нарисованными направлениями, как в точке 2, например? Почему он идет вообще непонятно с какой радости к центру? И, исходя из ваших объяснений, эти два пририсованные направления мы просто рисуем как касательную к окружности,а вторую - перпендикулярно первой. А зачем тогда нужны вообще данные уравнения и соответсвующие им знаки производных в каждом из квадрантов? Они тогда вообще не имеют смысла.
Последний раз редактировалось Dr. Arrieta 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
Индекс комплексного векторного поля
Своё понимание этих уравнений я высказал в посте 8. Ждем Андрея.Dr. Arrieta писал(а):Source of the post А зачем тогда нужны вообще данные уравнения и соответсвующие им знаки производных в каждом из квадрантов? Они тогда вообще не имеют смысла.
Последний раз редактировалось Рубен 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
Индекс комплексного векторного поля
Да, в рисунках ошибка. в точке 4 вектор должен смотреть вниз, а в точке 6 вверх. Я не стал проверять, ну потому что никогда не вдаюсь в такие частности, ну нашли ошибку, ну поправили.Тот не ошибается кто не работает)
Последний раз редактировалось Ian 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
Индекс комплексного векторного поля
Замечательный пример того, как с помощью ТФКП можно систему из двух ДУ свести к одному, да еще и с разделяющимися переменными.
Что интересно. Если эти уравнения записать в векторном виде, получится почти то же, что и в комплексном, только совершенно непригодное для дальнейшей работы:

где - неподвижные единичные орты вдоль действительной и мнимой осей соотвественно. Двойка при r и фи соотвествует возведению z в квадрат.
- неподвижные единичные орты вдоль действительной и мнимой осей соотвественно. Двойка при r и фи соотвествует возведению z в квадрат.
Что интересно. Если эти уравнения записать в векторном виде, получится почти то же, что и в комплексном, только совершенно непригодное для дальнейшей работы:
где
Последний раз редактировалось Рубен 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
Индекс комплексного векторного поля
Однако, ваш ребята искренний интерес к теме и меня немного заражает, вот если так бы было в разделах математики)
Решим что ли систему, то есть найдем все траектории

Что толкуется так, что левая дробь всегда действительное число. Интегрируем по t обе части.
 , где z_0 комплексное. После отображения 1/z траектории, значит, будут прямыми, параллельными действительной оси, значит, сами траектории ,из свойств инверсии -всевозможные окружности с выколотым нулем, касающиеся в 0 действительной оси
, где z_0 комплексное. После отображения 1/z траектории, значит, будут прямыми, параллельными действительной оси, значит, сами траектории ,из свойств инверсии -всевозможные окружности с выколотым нулем, касающиеся в 0 действительной оси
Решим что ли систему, то есть найдем все траектории
Что толкуется так, что левая дробь всегда действительное число. Интегрируем по t обе части.
Последний раз редактировалось Ian 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
- Dr. Arrieta
- Сообщений: 458
- Зарегистрирован: 02 авг 2009, 21:00
Индекс комплексного векторного поля
Так вот в этом-то моменте и загвоздка. Если мы принимаем, что в рисунке ошибка в этих двух точках, тогда индекс не получается равным 2, а он будет ноль. Т.е. мы считаем по направлениям, начиная от 1 и до 8 : если против часовой стрелки, то + угол, а если по, то -угол. Выходит, что:Ian писал(а):Source of the post Да, в рисунках ошибка. в точке 4 вектор должен смотреть вниз, а в точке 6 вверх. Я не стал проверять, ну потому что никогда не вдаюсь в такие частности, ну нашли ошибку, ну поправили.Тот не ошибается кто не работает)
ну и соответственно 0 делим на
Последний раз редактировалось Dr. Arrieta 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
Индекс комплексного векторного поля
А мне непонятно, что вы вообще делаете. Что это за углы и зачем вы их складываете и зачем результат потом делите наDr. Arrieta писал(а):Source of the post Выходит, что:ну и соответственно 0 делим на
получаем 0. Вот это-то мне и непонятно.
Последний раз редактировалось Рубен 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
- Dr. Arrieta
- Сообщений: 458
- Зарегистрирован: 02 авг 2009, 21:00
Индекс комплексного векторного поля
Для этого и задаются эти направления - чтобы потом посчитать на сколько произошло изменение и разделить на 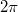 . Так и вычисляется индекс. Во всяком случае так было написано в моем учебнике и так нас этому учили в университете. Поэтому я и завис с этими направлениями - я пытался делать так, как это необходимо в теории, а правильный ответ не получается.
. Так и вычисляется индекс. Во всяком случае так было написано в моем учебнике и так нас этому учили в университете. Поэтому я и завис с этими направлениями - я пытался делать так, как это необходимо в теории, а правильный ответ не получается.
Последний раз редактировалось Dr. Arrieta 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
Индекс комплексного векторного поля
Нет там сумма 8 раз по П/2. Потому что при возрастании аргумента z на П/4 аргумент z^2 плавно растет на П/2Dr. Arrieta писал(а):Source of the post
Выходит, что:ну и соответственно 0 делим на
получаем 0. Вот это-то мне и непонятно.
Последний раз редактировалось Ian 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
- Dr. Arrieta
- Сообщений: 458
- Зарегистрирован: 02 авг 2009, 21:00
Индекс комплексного векторного поля
Получается, что везде где  и
и  надо брать
надо брать  ? И знаки тоже игнорируются? Т.е. направление вроде как по часовой стрелке и значит надо брать минус, а берется плюс, потому что z^2 растет?
? И знаки тоже игнорируются? Т.е. направление вроде как по часовой стрелке и значит надо брать минус, а берется плюс, потому что z^2 растет?
Мдаа...как-то это всё так шатко, так неупорядоченно - не видна какая-то цельная закономерность, всё везде с какими-то оговорками. Некрасивая, в общем, теория какая-то.
Мдаа...как-то это всё так шатко, так неупорядоченно - не видна какая-то цельная закономерность, всё везде с какими-то оговорками. Некрасивая, в общем, теория какая-то.
Последний раз редактировалось Dr. Arrieta 27 ноя 2019, 20:14, всего редактировалось 1 раз.
Причина: test
Причина: test
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 16 гостей