Здравствуйте! Задача имеет физическую подоплеку. Я произвожу измерения эффекта который пропорционален квадрату напряженности электрического поля. Прикладываю синусоидальный сигнал к кристаллу

. Образец при этом реагирует следующим образом:
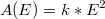
, то есть

, где
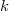
- некоторый коэффициент пропорциональности. Логично предположить, что частота измеряемого эффекта A при этом будет в два раза больше чем частота прикладываемого электрического поля E, потому как квадрат синуса равен 1, когда синус равен -1. Поэтому я и произвожу измерения на второй гармонике, то есть ловлю сигнал с образца с частотой
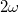
. Однако

это не то же самое что и

. Вопрос мой заключался в следующем: даже если основной вес сигнала и лежит на второй гармонике, а нет ли других более высоких гармоник в которые бьет
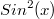
? Если так, то получается что я произвожу некорректные, или, если сказать точнее, неполные измерения.
Для того чтобы оценить насколько сильно влияют гармоники высшего порядка я и решил разложить

в ряд Фурье, чтобы оценить насколько весомы будут коэффициенты после
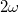
.
Но у меня ничего не получилось, давно я уже матаном не занимался. Воспользовался для начала онлайн калькулятором
http://www.kontrolnaya-rabota.ru/s/ryad/fure/http://www.kontrolnaya-rabota.ru/s/ryad/fure/ , но он завис на вопрос о разложении sin^2(x) или sin(x)*sin(x). Тогда взялся за бумагу и ручку.
Функция

является четной, поэтому ее можно раскладывать только по косинусам:



В результате я получил:
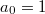
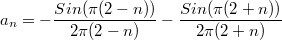
Второй член
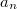
зануляется при любых значениях

, а первый зануляется при всех

, кроме
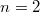
. А именно:

, это какой-то там замечательный предел, на сколько я помню, поэтому
 В итоге я получил простую тригонометрическую формулу:
В итоге я получил простую тригонометрическую формулу: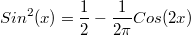
, только откуда-то во втором слагаемом у меня появилось лишнее
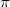
в знаменателе. Должно быть видимо так:
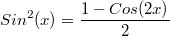
.
- Все выглядит очень правдоподобно, но неужели действительно
 при разложении не порождает никаких дополнительных гармоник кроме
при разложении не порождает никаких дополнительных гармоник кроме  ?
? - И еще подскажите где ошибка, которая привела к появлению лишнего
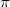 в знаменателе
в знаменателе
при разложении не порождает никаких дополнительных гармоник кроме
?
в знаменателе