Нашёл решение для
Ненадёжные весы
Ненадёжные весы
Даны чашечные весы, имеющие особенность — они могут выдержать ровно 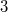 взвешивания (неважно в каком порядке) неравных грузов, после чего ломаются. Одинаковые веса можно уравновешивать на этих весах бесконечное количество раз. Среди
взвешивания (неважно в каком порядке) неравных грузов, после чего ломаются. Одинаковые веса можно уравновешивать на этих весах бесконечное количество раз. Среди 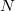 монет есть одна фальшивая, вес которой меньше настоящих. Найдите максимальное
монет есть одна фальшивая, вес которой меньше настоящих. Найдите максимальное 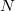 при котором можно найти фальшивую не более, чем за
при котором можно найти фальшивую не более, чем за 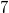 взвешиваний на этих весах.
взвешиваний на этих весах.
Нашёл решение для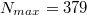 , строго обосновал и успокоился пока не узнал правильный ответ -
, строго обосновал и успокоился пока не узнал правильный ответ -
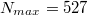 . Какая-то хитрость применена, не могу догадаться какая.
. Какая-то хитрость применена, не могу догадаться какая.
Нашёл решение для
Последний раз редактировалось Таланов 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
Похоже или что-то не то с условиями или с ответом.
Для 379 несложно решить, первый раз надо по 73 взвешивать.
Ну и для общего случая - сколько всего взвешиваний и сколько неравновесных допустимо тоже знаю решение - типа паскалевского треугольника.
А вот 527 в нём всего один раз встречается - если ровно одно неравновесное взвешивание, а всего не более 263
Для 379 несложно решить, первый раз надо по 73 взвешивать.
Ну и для общего случая - сколько всего взвешиваний и сколько неравновесных допустимо тоже знаю решение - типа паскалевского треугольника.
А вот 527 в нём всего один раз встречается - если ровно одно неравновесное взвешивание, а всего не более 263
Последний раз редактировалось СергейП 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
Ответы на головоломки в IQ-календаре 2013 «Профессор» 5. Май.
[url=http://stprofessor.ru/filosofiya/otvety-na-golovolomki/]http://stprofessor.ru/filosofiya/otvety-na-golovolomki/[/url]
Последний раз редактировалось Таланов 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
Интересно посмотреть решение для которого у тебя лично IQ недостаточен.
Последний раз редактировалось Таланов 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
Вместо 3 и 7 берём соответственно  и
и  . Соответствующее максимальное значение обозначим
. Соответствующее максимальное значение обозначим 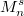 . При каждом взвешивании
. При каждом взвешивании  либо не меняется либо уменьшается на единицу, а
либо не меняется либо уменьшается на единицу, а  уменьшается на 1. Отсюда очевидна рекуррентность:
уменьшается на 1. Отсюда очевидна рекуррентность: 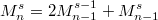 - похоже на треугольник Паскаля.
- похоже на треугольник Паскаля.
Краевые условия: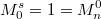 .
.
Краевые условия:
Последний раз редактировалось bot 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
Ага!bot писал(а):Source of the post Вместо 3 и 7 берём соответственнои
. Соответствующее максимальное значение обозначим
. При каждом взвешивании
либо не меняется либо уменьшается на единицу, а
уменьшается на 1. Отсюда очевидна рекуррентность:
- похоже на треугольник Паскаля.
Краевые условия:.
Именно так и заполнил табличку в кселе минут за 5.
Ещё добавлю - количество взвешиваемых на каждой чашке камней -
Последний раз редактировалось СергейП 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
Я тоже заполнил:

Если взвешивание равновесное, двигаемся вправо, в противном случае вниз.
Но как найти решение для
Последний раз редактировалось Таланов 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
По реккурентности очевидно максимум. А что по ней такое число не вылазит? Ну, тогда так тому и быть - никак.
PS. Реккурентность приведёт к многочлену степени
Последний раз редактировалось bot 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
То что заполнил - хорошо, но если бы ещё при этом стало понятно о чём речь - было бы ещё лучше.Таланов писал(а):Source of the post Я тоже заполнил:
Если взвешивание равновесное, двигаемся вправо, в противном случае вниз.
Но как найти решение для?
Вот табличка о которой шла речь

В столбце А кол-во взвешиваний, а в 1-ой строке - допустимое число неравновесных взвешиваний.
На пересечении - максимальное
Искомое число
Последний раз редактировалось СергейП 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Ненадёжные весы
bot писал(а):Source of the post
По реккурентности очевидно максимум. А что по ней такое число не вылазит? Ну, тогда так тому и быть - никак.
Нам голову морочат и быть такого не может?
Последний раз редактировалось Таланов 27 ноя 2019, 21:35, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 5 гостей