Нет (тема продолжается и поныне).
Корны, Бермант-Араманович о производной по направлению.
Корны, Бермант-Араманович о производной по направлению.
Последний раз редактировалось Рубен 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
Корны, Бермант-Араманович о производной по направлению.
Последний раз редактировалось kkdil 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
-
Орбан И.Н.
- Сообщений: 16
- Зарегистрирован: 16 дек 2013, 21:00
Корны, Бермант-Араманович о производной по направлению.
1) Вы противоречите сами себе, то вопрошая в каких справочниках идет речь об ортогональности 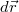 и
и 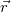
то отвечая (действительно, самому себе)
об ортогональности вектора касательной к поверхности уровня
касательной к поверхности уровня 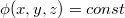 плоскости, в которой и лежит вектор
плоскости, в которой и лежит вектор 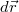 , так как в данном случае
, так как в данном случае 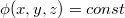 при
при 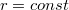 , следовательно
, следовательно 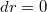 .
.
2) То, голословно обвиняя кого-то в демагогии, заявляете о неких ложных предположениях, не указывая таковых и попросту игнорируете предоставленное Вам математическое доказательство коллинеарности в этой ситуации векторов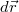 и
и 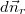 :
:

 .
.
Так как векторное произведение векторов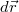 и
и 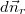 равно нулю, следовательно они коллинеарны.
равно нулю, следовательно они коллинеарны.
3) То приводите не относящийся к обсуждаемому случаю пример эллипсоида, так и не порадовав функцией потенциала скалярного поля, для которого эквипотенциальными поверхностями, то есть геометрическими местами точек, в которых скалярное поле принимает постоянные значения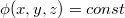 , являлись бы эллипсоиды. Вместо этого задаете глупые вопросы:
, являлись бы эллипсоиды. Вместо этого задаете глупые вопросы:
Уверен, что это является для Вас откровением, но функция потенциала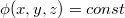 скалярного поля принимает постоянные значения тогда и только тогда, когда
скалярного поля принимает постоянные значения тогда и только тогда, когда 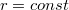 . Других вариантов постоянства зависящей от расстояния функции
. Других вариантов постоянства зависящей от расстояния функции 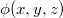 математике неизвестны.
математике неизвестны.
Если Вы знаете еще какие-либо, отличные от постоянства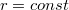 , условия постоянства
, условия постоянства 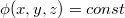 , которые до сих пор математике были неизвестны, то милости прошу, не скрывайте этого своего уникального открытия и не держите его в себе, поделитесь на форуме с читателями!
, которые до сих пор математике были неизвестны, то милости прошу, не скрывайте этого своего уникального открытия и не держите его в себе, поделитесь на форуме с читателями!
4) Наконец, как можно судить по материалам дискуссии, я прекрасно понял, что Вы опровергали и продолжаете голословно опровергать
ортогональность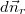 и
и  . Доказательства же от Вас Ваших голословных заверений, что вектора
. Доказательства же от Вас Ваших голословных заверений, что вектора 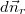 и
и  не являются ортогональными, до сих пор так не последовало!
не являются ортогональными, до сих пор так не последовало!
Когда же Вы докажете хотя бы это свое высказывание, без которого все Ваши так называемые "возражения" - не более, чем бездоказательная демагогия?
Рубен писал(а):Source of the post
Какое такое условие ортогональностии
? В каких справочниках? Вы вообще о чем?
то отвечая (действительно, самому себе)
Рубен писал(а):Source of the post
Действительно, вектор-функцияортогональна касательной плоскости, проходящей через точку (x,y,z) (это известный факт и доказательство этому можно прочесть в любом учебнике анализа). Так как приращение
радиус-вектора
вдоль любой линии на поверхности
всегда лежит в касательной плоскости к
, то
.
об ортогональности вектора
2) То, голословно обвиняя кого-то в демагогии, заявляете о неких ложных предположениях, не указывая таковых и попросту игнорируете предоставленное Вам математическое доказательство коллинеарности в этой ситуации векторов
Так как векторное произведение векторов
3) То приводите не относящийся к обсуждаемому случаю пример эллипсоида, так и не порадовав функцией потенциала скалярного поля, для которого эквипотенциальными поверхностями, то есть геометрическими местами точек, в которых скалярное поле принимает постоянные значения
Уверен, что это является для Вас откровением, но функция потенциала
Если Вы знаете еще какие-либо, отличные от постоянства
4) Наконец, как можно судить по материалам дискуссии, я прекрасно понял, что Вы опровергали и продолжаете голословно опровергать
Рубен писал(а):Source of the postЭто утверждение ... неверно.Вектор... естественно ортогонален направлению вектора
.
ортогональность
Когда же Вы докажете хотя бы это свое высказывание, без которого все Ваши так называемые "возражения" - не более, чем бездоказательная демагогия?
Последний раз редактировалось Орбан И.Н. 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
Корны, Бермант-Араманович о производной по направлению.
Уже задрал оверквотинг...
Пересмотрел все - нигде не нашел, чтоб ставили условие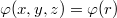 ...
...
Очередная очепятка?
Пересмотрел все - нигде не нашел, чтоб ставили условие
Очередная очепятка?
Последний раз редактировалось kiv 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
Корны, Бермант-Араманович о производной по направлению.
Еще раз спрашиваю, откуда условие
Это не доказательство, так как выкладки неверны. Конкретно эта часть:и попросту игнорируете предоставленное Вам математическое доказательство коллинеарности в этой ситуации векторови
:
.
так как
Кто вам сказал этот дикий бред ? Вас обманули!Вместо этого задаете глупые вопросы:
Уверен, что это является для Вас откровением, но функция потенциаласкалярного поля принимает постоянные значения тогда и только тогда, когда
.
Я уже поделился в примере с элипсоидом, только вот вы этого не поняли, а остальные читатели - поняли. Ну, почитайте еще разок, может увидите наконец и поймете (в чем я сильно сомневаюсь).Других вариантов постоянства зависящей от расстояния функцииматематике неизвестны.
Если Вы знаете еще какие-либо, отличные от постоянства, условия постоянства
, которые до сих пор математике были неизвестны, то милости прошу, не скрывайте этого своего уникального открытия и не держите его в себе, поделитесь на форуме с читателями!
На каком основании вы накладываете на функцию такие жесткие условия? Функция потенциала не обязана зависеть от расстоянияДругих вариантов постоянства зависящей от расстояния функцииматематике неизвестны.
Ponomaryov писал(а):Source of the post С Вами будем продолжать, когда Вы докажете неверность в общем случае моего утверждения об ортогональности ВО ВСЕХ СЛУЧАЯХ векторови
, прописанного ВО ВСЕХ СПРАВОЧНИКАХ.
Если это окажется "опечаткой", то топикстартер отправится в долгосрочный отпуск учиться формулировать задачи.kiv писал(а):Source of the post Пересмотрел все - нигде не нашел, чтоб ставили условие...
Очередная очепятка?
Кстати, для подтверждения / опровержения этого сам топикстартер должен появиться в теме, ответ его зама по поводу того, что имел ввиду топикстартер - не принимается
Проблемы с логикой? Вылечим! К вашему сожалению, это вы должны "доказывать", что носорог является бегемотом (а не я доказывать обратное). Ваше "доказательство" того, что эти вектора ортогональны основано на ложном предположении, что вдоль поверхности уровняОрбан И.Н. писал(а):Source of the post Доказательства же от Вас Ваших голословных заверений, что вектораи
не являются ортогональными, до сих пор так не последовало!
Последний раз редактировалось Рубен 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
Корны, Бермант-Араманович о производной по направлению.
Ponomaryov писал(а):Source of the post
Дальше продолжим, когда обоснуете математическую безупречность того, как "работает" последнее вытекающее из обсуждаемого общепринятого определения производной по направлению определение косинуса угламежду векторами
и
.
Самое смешное то, что первое равенство в общем случае неверно (верно, если поверхность уровня -- n-мерная сфера), а второе - верно всегда. Причем, второе вообще никак не связано с первым, более того, оно вполне очевидно и доказывается без всяких дурацких градиентов.
1) Совершенно ясно, что вектора
2) То же самое, но более формально. Производная радиус-вектора по любому направлению
Скалярно умножаем последнее равенство на
3) Еще, для разнообразия, это можно доказать через уравнение прямой в векторной форме. Расстояние
тут
_____________________________________________
Единственное, что так и осталось неясным, что же всё-таки хотел ниспровергнуть ТС в этой теме?
Последний раз редактировалось Рубен 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
-
Орбан И.Н.
- Сообщений: 16
- Зарегистрирован: 16 дек 2013, 21:00
Корны, Бермант-Араманович о производной по направлению.
Это условие оттуда, что Вы так и не привели математического примера постоянства зависящих от расстояния функций
Следовательно, для случая
Хотя, это стало уже вполне традиционным для Вас - противоречить самому себе, как в случае с Вашими взаимоисключающими высказываниями
Рубен писал(а):Source of the postЭто верно.Вектор, по общеизвестному определению ортогональности призводной вектора постоянного модуля самому вектору
Это утверждение ... неверно.Вектор... естественно ортогонален направлению вектора
.
Сообщаю, что, к огромному Вашему сожалению, если Вы признаете ортогональность производной единичного вектора постоянного модуля
Рубен писал(а):Source of the post
Действительно, вектор-функцияортогональна касательной плоскости, проходящей через точку (x,y,z) (это известный факт и доказательство этому можно прочесть в любом учебнике анализа). Так как приращение
радиус-вектора
вдоль любой линии на поверхности
всегда лежит в касательной плоскости к
, то
.
условием
Если
то
Следовательно, выражение (*), вполне логично, как раз и подтверждает равенство нулю
А так как Вы до сих пор не порадовали другим, кроме
Итак, когда же Вы начнете обосновывать собственные высказывания и докажете, что утверждение об ортогональности векторов
Последний раз редактировалось Орбан И.Н. 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
Корны, Бермант-Араманович о производной по направлению.
"Вы не привели" не может быть основанием верности ваших предположений. Оппонент не обязан доказывать ложность ваших фантазий. Но я доказал.Орбан И.Н. писал(а):Source of the post Это условие оттуда, что Вы так и не привели
Вы так и не привели математического примера постоянства зависящих от расстояния функций, кроме
. Пока Вы не порадовали другим, кроме
, условием постоянства
, оно в математике было, есть и остается единственным, к сожалению для Вас.
Вот он - этот пример. Если он вас не устраивает, вы обязаны аргументировать это.
Вся остальная ваша болтовня в предыдущем посте никакого интереса не представляет, т.к. основана на ложном посыле, что если
Последний раз редактировалось Рубен 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
-
Орбан И.Н.
- Сообщений: 16
- Зарегистрирован: 16 дек 2013, 21:00
Корны, Бермант-Араманович о производной по направлению.
Рубен писал(а):Source of the postНа каком основании вы накладываете на функцию такие жесткие условия? Функция потенциала не обязана зависеть от расстоянияДругих вариантов постоянства зависящей от расстояния функцииматематике неизвестны.
. Мы с топикстартером обсуждали функцию общего вида, о чем не раз подчеркивалось в теме как мною, так и самим топикстартером:
Ponomaryov писал(а):Source of the post С Вами будем продолжать, когда Вы докажете неверность в общем случае моего утверждения об ортогональности ВО ВСЕХ СЛУЧАЯХ векторови
, прописанного ВО ВСЕХ СПРАВОЧНИКАХ.
Вы неисправимы в искусстве противоречить самому себе, это стоит признать:
Рубен писал(а):Source of the post
Тут проверять нечего:
или
Это все "работает", если функция дифференцируема в точке (x,y,z).
"Функция потенциала не обязана зависеть от расстояния r. Мы с топикстартером обсуждали функцию общего вида" (с) Рубен
"Это все "работает", если функция дифференцируема в точке (x,y,z)" (с) Рубен
Вы в обсуждении с топикстартером привели пример дифференцирования по направлению не зависящей от расстояния функции
Вы действительно верите, что Ваше систематическое противоречие самому себе и Ваши традиционные опровержения собственных высказываний на форуме являются доказательством неортогональности
"Каждому дано будет по его вере." Мастер и Маргарита.
Рубен писал(а):Source of the post"Вы не привели" не может быть основанием к вашим фантазиям. Оппонент не обязан доказывать ложность ваших фантазий.Орбан И.Н. писал(а):Source of the post Это условие оттуда, что Вы так и не привелиВы так и не привели математического примера постоянства зависящих от расстояния функций, кроме
. Пока Вы не порадовали другим, кроме
, условием постоянства
, оно в математике было, есть и остается единственным, к сожалению для Вас.
Привел. Вот этот пример. Если он вас не устраивает, вы обязаны аргументировать это.
Вся остальная ваша болтовня в последнем посте никакого интереса не представляет, т.к. основана на ложном посыле, что если, то
.
Для приведенного Вами примера модуль
Следовательно, посыл Вас к здравому смыслу, математически формулируемому здесь как
тогда и только тогда
является истинным, голосу которого Вы внять упорно отказываетесь, так как Ваш эллипсоид условию
Хотя, оговорюсь, для кого-то (например для Вас), математическим доказательством является его регулярная голословная демагогия. Имеет право получать удовольствие в меру Вашего развития, это Ваше право, действительно, никто отобрать у Вас не в состоянии.
Последний раз редактировалось Орбан И.Н. 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
Корны, Бермант-Араманович о производной по направлению.
Конечно. Это функция точки, а не расстояния. Расстояние может не меняться, а функция менять своё значение и наоборот: расстояние меняется, а функция сохраняет своё значение. Пример я уже приводил: половина эллипсоида.Орбан И.Н. писал(а):Source of the post Вы в обсуждении с топикстартером привели пример дифференцирования по направлению не зависящей от расстояния функции?
Как же не удовлетворяет, когда она (функция) всюду равна 0,5. Взяли эллипсоид и срезали плоскостью, параллельной плоскости OXY на расстоянии 0,5 от неё. Вот и получили поверхность уровня - эллипс.Для приведенного Вами примера модуль, следовательно, поверхность эллипсоида не удовлетворяет свойству поверхности уровня, а именно
.
Вы просили контрпример - вы его получили. Теперь нечего топать ножками
Последний раз редактировалось Рубен 28 ноя 2019, 06:38, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Альтернативная наука»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 29 гостей