Такая ситуация. Есть задача: построить выводы секвенций в ИС:
(б) (A->B),(B->C)|-(A->C)
Нужно использовать 15 формул. Правила вывода:
Г1 |- A; Г 2 |- B
________________________________
Г1, Г2 |- (A&B)
и т.д.
Я не могу понять: как их использовать и что куда откуда следует.
Сверху вниз или снизу вверх в правилах вывода идет... не следствие... а вывод что ли.
А когда я решаю. мне как эти правила применять? Снизу вверх или сверху вниз?
А почему? И зачем при решении все это дело записывать снизу вверх, это же неудобно!
Исчисления Высказываний
Исчисления Высказываний
Последний раз редактировалось walkrunm 28 ноя 2019, 13:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Исчисления Высказываний
Это значит что у вас есть два утверждения A->B и B->C и из них выводится A->C
Г1 |- A; Г 2 |- B
________________________________
Г1, Г2 |- (A&B)
Это значит что если у вас есть вывод А из набора посылок Г1 и вывод B из набора Г2 то из объединения
Г1,Г2 можно вывести (A&B) - в общем то очевидно.
То что над чертой это набор выводов а под чертой новый вывод который из них вытекает.
Если вы пишете снизу вверх то вы идете от цели пытаясь разбить ее на кусочки, если пишете сверху вниз - то идете от мелких утверждений к вашей теореме - используются оба подхода. Возьмите классический учебник по логике - там все это расписано с прекрасными примерами. Вкурить не видев ни разу вывода в таком духе непросто.
Я бы рекомендовал Клини С. К. "Математическая логика" там неспешно с примерами все рассказывается.
Есть еще система HOL в которой такие доказательства сами собой получаются, но разбираться с ней... В общем не рекомендую если мало времени, но если хотите наоборот разобраться в деталях - очень даже хорошая документация и программа. Если разберетесь в HOL то логика вам точно не страшна)
Последний раз редактировалось folk 28 ноя 2019, 13:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Исчисления Высказываний
Формулы надо оформлять  ом, конъюнкция пишется \&:
ом, конъюнкция пишется \&: 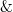 , дизъюнкция \vee:
, дизъюнкция \vee: 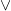 , вывод \vdash:
, вывод \vdash: 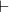 .
.
Нужно указать систему аксиом. Нужно явно указать правила вывода. Только потом сможете построить вывод. Чтобы понять, как доказывать, просто посмотрите определение вывода формулы.
Если все равно непонятно, можете скачать Игошина, теорию и задачник, там все очень подробно расписано с примерами.
Нужно указать систему аксиом. Нужно явно указать правила вывода. Только потом сможете построить вывод. Чтобы понять, как доказывать, просто посмотрите определение вывода формулы.
Если все равно непонятно, можете скачать Игошина, теорию и задачник, там все очень подробно расписано с примерами.
Последний раз редактировалось Sonic86 28 ноя 2019, 13:39, всего редактировалось 1 раз.
Причина: test
Причина: test
-
Импровизатор
- Сообщений: 37
- Зарегистрирован: 17 фев 2012, 21:00
Исчисления Высказываний
walkrunm писал(а):Source of the post
Такая ситуация. Есть задача: построить выводы секвенций в ИС:
(б) (A->B),(B->C)|-(A->C)
Нужно использовать 15 формул. Правила вывода:
Г1 |- A; Г 2 |- B
________________________________
Г1, Г2 |- (A&B)
и т.д.
Я не могу понять: как их использовать и что куда откуда следует.
Сверху вниз или снизу вверх в правилах вывода идет... не следствие... а вывод что ли.
А когда я решаю. мне как эти правила применять? Снизу вверх или сверху вниз?
А почему? И зачем при решении все это дело записывать снизу вверх, это же неудобно!
тут импликация A->B = не-А V B
Из-за нее вывод довольно длинноват будет.
Последний раз редактировалось Импровизатор 28 ноя 2019, 13:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Дискретная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость