Что вы всегда хотели узнать, но боялись спросить

Swetlana · Сообщение **Swetlana** » 20 янв 2013, 15:23

глянула Кормена, как там определяется погрешность приближённого алгоритма задачи минимизации (см. опр. **), попроще чем в Гэри-Джонсоне

Определение *. Алгоритмы, генерирующие квазиоптимальные решения за полиномиальное время, называются приближенными алгоритмами.
(делаем акцент на том, что наши "хорошие" неоптимальные решения будем генерировать за полиномиальное время)

Первый тип оценок погрешности приближенных алгоритмов – это гарантированные оценки точности получаемого решения «в наихудшем случае». Часто для оценки погрешности приближенного алгоритма «в наихудшем случае» используется следующее определение.
Определение **. $$A$$

- алгоритм называется $$C(n)$$

- приближенным, если для любых исходных данных размера $$n$$

он находит допустимое решение со значением целевой функции, отличающимся от оптимума не более чем в $$C(n)$$

раз.
Таким образом, алгоритм является $$C(n)$$

- приближенным, если
$max \left \{R_A(I) = \frac{A(I)}{OPT(I)} \right \} \leq C(n)$ , максимум ищется по всем возможным наборам исходных данных $$I$$

.

Величина $$C(n)$$

– мультипликативная ошибка, показывающая во сколько раз величина приближенного решения отличается от оптимума в самом плохом случае.
Мультипликативная ошибка может быть константой или зависеть от параметров входа $$I$$

.

Swetlana · Сообщение **Swetlana** » 20 янв 2013, 19:40

Сообщение отредактировано

Ув. коллеги, давайте вернёмся к двум разным определениям безразмерной погрешности приближённого алгоритма, у Гэри-Джонсона и Кормена.

Поняла, наконец, что мне не нравится, в обоих определениях.
Определение Кормена некорректно, из-за недостаточной строгости.
А Гэри-Джонсон излишне "заложились" (как преферансисты говорят ), их определение можно упростить.
Вот, смотрите сами.

Определение (Кормен). $$A$$

- алгоритм называется $$C(n)$$

- приближенным, если для любых исходных данных размера $$n$$

он находит допустимое решение со значением целевой функции, отличающимся от оптимума не более чем в $$C(n)$$

раз.
Таким образом, алгоритм является $$C(n)$$

- приближенным, если
$max \left \{R_A(I) = \frac{A(I)}{OPT(I)} \right \} \leq C(n)$ , максимум ищется по всем возможным наборам исходных данных $$I$$

.

Максимум берётся от левой части неравенства, от $$R_A(I)$$

, по всем индивидуальным задачам, которых, вообще-то бесконечно.
У бесконечного множества максимум не обязан существовать. Здесь должен быть супремум $$sup$$

- наименьшая из всех верхних граней.

Определение (Гэри-Джонсон). Погрешностью приближённого алгоритма $$A$$

решения задачи $$Ï$$ назовём величину $$R_A$$

:
$$R_A = inf \left\{ r \geq 1: \ R_A(I) \leq r \ äëÿ \ âñåõ \ I \in D_Ï \right \}$$.

Инфинум inf берётся от правой части равенства, не от $$R_A(I)$$

, а от его мажоранты, которая может быть равна бесконечности... уроборосу :rolleyes:
Зачем здесь инфинум??? достаточно обычного минимума

Swetlana · Сообщение **Swetlana** » 21 янв 2013, 10:32

... отбрасываем первое определение как некорректное (или пусть мне докажут его корректность), которым сейчас пользуются все , и продолжаем обсуждать определения Гэри-Джонсона.

Очевидно, что погрешность алгоритма $$R_A$$

не может быть равна 1 - иначе бы для всех индивидуальных задач выполнялось бы $$Opt(I) = A(I)$$

, и алгоритм $$A$$

был бы точным алгоритмом.

А вот асимптотическая погрешность $R_A^{\infty}$ может быть равна 1, не для всех индивидуальных задач, а только для задач с достаточно большой величиной решения.

Определение 6. Для оптимизационной задачи $$Ï$$ назовём асимптотически наилучшей достижимой относительной погрешностью величину $$R_{MIN}(Ï): $$ <span class=

$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">R_{MIN}(Ï) = inf \left \{ r \geq 1: \ äëÿ \ ðåøåíèÿ \ çàäà÷è \ Ï \ $$ <span class=

$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">ñóùåñòâóåò \ òàêîé \ ïðèáëèæ¸ííûé \ ïîëèíîìèàëüíûé \ àëãîðèòì \ A, \ $$ <span class=

$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">÷òî \ R_A^{\infty} = r \left \} $$

Перечислим три основных типа оценок погрешности приближённых алгоритмов.
$$1.$$

$$R_{MIN}(Ï) = \infty $$. <span class=

$$" title="$$. $$" align="middle" style="border: 0; vertical-align: middle">2. $$ <span class=

$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">1 < R_{MIN}(Ï) < \infty $$. <span class=

$$" title="$$. $$" align="middle" style="border: 0; vertical-align: middle">3. $$ <span class=

$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">R_{MIN}(Ï) = 1$$.

Если $$R_{MIN}(Ï) = 1$$, то можно выделить ещё 4 важных подслучая.
Задача $$Ï$$ может быть решена:
 $$1.$$

полиномиальной приближенной схемой (PTAS);
 $$2.$$

вполне полиномиальной приближенной схемой (FPTAS);
 $$3.$$

приближенным полиномиальным алгоритмом $$A$$

с асимптотической погрешностью $R_A^{\infty} = 1$ ;
 $$4.$$

приближенным полиномиальным алгоритмом $$A$$

, для которого при некотором фиксированном $$K$$

выполнено неравенство $$|A(I) OPT(I)| \leq K$$ для любого входа $$I$$

.

Swetlana · Сообщение **Swetlana** » 22 янв 2013, 09:22

Определение (Гэри-Джонсон). Погрешностью приближённого алгоритма $$A$$

решения задачи $$Ï$$ назовём величину $$R_A$$

: $$R_A = inf \left\{ r \geq 1: \ R_A(I) \leq r \ äëÿ \ âñåõ \ I \in D_Ï \right \}$$.

эта... пусть множество $$M = \{ R_A(I), \ I \in \D_Ï \}$$
для каждого элемента множества M берём мажоранту
получаем множество верхних граней множества $$M$$

затем из всех верхних граней надо выбрать минимальный элемент
зачем здесь инфинум???

открывая эту тему, планировала внести хоть и малозначимый, но свой, вклад в борьбу с невежеством и мракобесием
вот сейчас, наконец, стало ясно, что эту борьбу надо начинать с себя
----------------------------------------------------------------------------------------------------------------------------

Полиномиальные апроксимационные схемы, PTAS
(читается питас)

Полиномиальная апроксимационная схема - это набор или серия полиномиальных алгоритмов.
Идея апроксимационной схемы очень проста: для каждого фиксированного $\epsilon > 0$ получаем полиномиальный алгоритм $A_{\epsilon}$ с погрешностью, не превосходящей $1 + \epsilon : \ R_{A_{\epsilon}} \leq 1+\epsilon$ .
Время работы такого алгоритма зависит от погрешности - чем меньше погрешность, тем дольше будет работать алгоритм.

Определение 7. Назовём апроксимационной схемой для оптимизационной задачи $$Ï$$ алгоритм $$A$$

, который, начиная работать на входе, состоящем из двух объектов - индивидуальной задачи $$I \in D_Ï$$ и заданной погрешности $\epsilon$ , выдаёт такое допустимое решение $$\sigma \in S_Ï(I)$$, что $\ R_{A_{\epsilon}}(I) \leq 1+\epsilon$ , или $\frac{A_{\epsilon}(I)}{OPT(I)} \leq 1+\epsilon$ (для задачи минимизации).

Определение 8. Приближённая схема $$A$$

называется приближённой полиномиальной (апроксимационной) схемой (PTAS), если для каждого фиксированного $\epsilon > 0$ соответствующий алгоритм $A_{\epsilon}$ имеет полиномиальную временную сложность.

Определение 9. Приближённая схема $$A$$

называется вполне полиномиальной приближённой схемой (FPTAS), если её временная сложность ограничена полиномом от $$Length(I)$$

и $\frac{1}{\epsilon}$ .

всё это, разумеется, непонятно, без примеров
как все псевдополиномиальные алгоритмы получаются из динамического программирования, так почти все полиномиальные апроксимационные схемы получаются масштабированием (с последующим округлением) исходных данных в псевдополиномиальных алгоритмах
примеры будут, чуть позже

Swetlana · Сообщение **Swetlana** » 22 янв 2013, 14:36

Большая размерность

возьмём для примера модельную задачу "Сумма размеров", но в реальной размерности
реальная задача об оперативном планировании отгрузки готовой листопрокатной продукции многокритериальная, выделим только один параметр - вес, и один критерий - набрать заданный вес с минимальным отклонением по модулю

Типичный вариант отгрузки - десять вагонов готовой продукции - составляет примерно $$n = 200$$

пачек, массы пачек $$s(a)$$

заданы в кг, масса отгружаемой продукции $$B = 620000êã$$, допустимое отклонение $$\pm 2000 êã$$.
Для ДП эта размерность слишком велика, более того, оперативное планирование отгрузки должно занимать секунды.

Попробуем применить метод масштабирования для динамического программирования.
Метод заключается в уменьшении всех заданных величин $$s(a)$$

и

в

раз, где

– коэффициент масштабирования, и последующим округлением до целого путем отбрасывания дробной части. Величина погрешности полученного таким образом решения не превосходит $$n*scale$$

.

Применим метод масштабирования к типичному варианту отгрузки. В задаче об отгрузке погрешность набора веса является исходным данным и не должна превосходить $$2000 êã$$, отсюда $n*scale \leq 2000$ . Для нашего примера получаем $200*scale \leq 2000$ , откуда $scale \leq 10$ , что не дает существенного выигрыша в быстродействии.
Время работы алгоритма $O(n* \frac{B}{scale})$ .

Swetlana · Сообщение **Swetlana** » 24 янв 2013, 21:16

Масштабирование для задачи о рюкзаке
...продолжаем упражняться в масштабировании полиномиальных и псевдополиномиальных алгоритмов

На этот раз в качестве модельной задачи возьмём задачу "Рюкзак".
Дано конечное множество предметов $$A$$

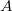
, каждый предмет имеет целый положительный вес $$w(a)$$

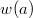
и стоимость $$s(a)$$

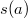
, задано целое положительное число $$B$$

- ограничение на вес рюкзака. Требуется упаковать в рюкзак выборку предметов максимальной ценности, удовлетворяющую ограничению на вес рюкзака.
В скобках замечу, что если положить, что вес предмета равен его стоимости ( $$w(a) = s(a)$$

), то из "Рюкзака" получим задачу "Сумма размеров", где $$B$$

- максимальная возможная стоимость, которую мы пытаемся набрать.

В качестве алгоритма её решения возьмём псевдополиномиальный алгоритм ДП.

Будем считать, что очень большими в этой задаче могут быть стоимости.
Разделим все стоимости $$s(a)$$

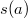
на

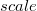
, где

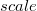
– коэффициент масштабирования, и округлим до целого путем отбрасывания дробной части.
Стоимость любого предмета в модифицированной задаче отличается от исходной стоимости не более чем на $$scale$$

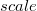
. В оптимальном решении может быть не более, чем $$n$$

предметов, поэтому величина суммарной погрешности не превосходит $$n*scale$$

.

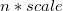
Пусть

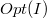
- стоимость оптимального рюкзака,
$Opt(I^{'})$ - стоимость оптимального рюкзака масштабированной задачи.
Умножаем оптимальную стоимость масштабированного рюкзака на коэффициент масштабирования и получаем величину приближённого решения $A(I) = scale*Opt(I^{'})$ .
Величина оптимального решения отличается от величины приближённого не более чем на $$n*scale$$

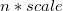
: $Opt(I)-A(I) = Opt(I)-scale*Opt(I^{'}) \leq n*scale$ . (задача на максимум, оптимальная стоимость больше приближённой)
Коэффициент масштабирования можно взять так, как нам удобно.
Пусть $scale = \frac{Opt(I)}{(k+1)n}$ , где $$k$$

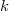
- фиксированное целое положительное число, теперь величина приближённого решения зависит от $$k$$

.
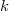
Получаем $Opt(I) - A_k(I) \leq \frac{Opt(I)}{k+1}$ или
$A_k(I) \geq Opt(I) - \frac{Opt(I)}{k+1}$ .
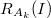
Отсюда коэффициент относительной погрешности $R_{A_k}(I)$ равен, после несложных преобразований:
$R_{A_k}(I) = \frac{Opt(I)}{A_k(I)} \leq 1 + \frac{1}{k}= 1 + \epsilon$ .

Вычислительная сложность алгоритма ДП для исходной задачи равна $$O(nB)$$

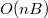
или

.
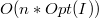
Вычислительная сложность решения отмасштабированной задачи равна
$O( \frac {nOpt(I)}{\frac{Opt(I)}{(k+1)n}}) = O(n^{2}*k) = O(\frac{n^{2}}{\epsilon})$ .

Теперь вспоминаем определение вполне полиномиальной приближённой схемы
Приближённая схема $$A$$

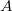
называется вполне полиномиальной приближённой схемой (FPTAS), если её временная сложность ограничена полиномом от $$Length(I)$$

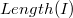
и $\frac{1}{\epsilon}$ .

Мы получили вполне полиномиальную приближённую схему, для задачи о рюкзаке, и для задачи "Сумма размеров".

Swetlana · Сообщение **Swetlana** » 25 янв 2013, 11:18

Swetlana писал(а):Source of the post
Коэффициент масштабирования можно взять так, как нам удобно.
Пусть $scale = \frac{Opt(I)}{(k+1)n}$ , где - фиксированное целое положительное число...

В момент масштабирования величину оптимального решения $$Opt(I)$$

мы не знаем, увы
поэтому
Вместо $$Opt(I)$$

нужно взять величину приближённого решения $$GA(I)$$

, полученную известным "жадным" (greedy) алгоритмом.
Про него (greedy algorithm) известно, что величина решения $$GA(I)$$

не более чем в $$2$$

раза отклоняется (меньше) от величины оптимального решения, а коэффициент $$2$$

уйдёт в константу О_большое.

Теперь надо про этот greedy algorithm для рюкзака рассказать, и заодно и его отмасштабировать, другим разом...

Swetlana · Сообщение **Swetlana** » 27 янв 2013, 13:22

Задача о рюкзаке. Жадные алгоритмы. Оценки относительной погрешности.

Жадный алгоритм.
1. Отсортируем предметы в порядке убывания их относительной стоимости (стоимости 1 кг):
$\frac{s_1(a)}{w_1(a)} \geq \frac{s_2(a)}{w_2(a)} \geq \dots \frac{s_n(a)}{w_n(a)}$ .
2. Начнём с пустого рюкзака. Будем добавлять к нему предметы в порядке возрастания номеров. Если предмет проходит ограничение на вес рюкзака, он добавляется, иначе - отбрасывается.

Покажем, что мультипликативная погрешность такого алгоритма не ограничена сверху,
т.е. не существует $$C > 0$$

, такой, что для всех индивидуальных задач $$I:$$

$\frac{Opt(I)}{GA(I)} \leq C.$

NT · Сообщение NT » 27 янв 2013, 13:38

Swetlana писал(а):Source of the post Покажем, что мультипликативная погрешность такого алгоритма не ограничена сверху,
т.е. не существует , такой, что для всех индивидуальных задач
$\frac{Opt(I)}{GA(I)} \leq C.$

Не понял, а если вместимость рюкзака 1 кг, всего предметов 10.
И них самый дорогой и самый тяжелый акурат - брусок золота весом 1 кг.
То как тогда с С?

Swetlana · Сообщение **Swetlana** » 27 янв 2013, 14:02

<dummy>

yourdomain.com