Что вы всегда хотели узнать, но боялись спросить

[Swetlana]

Сильная -полнота

Итак, схему кодирования считают разумной, если она не позволяет искусственного "раздувания" входа. Раздувание может привести к такому увеличению длины входного слова, что экспоненциальный алгоритм может превратиться в полиномиальный.
Как мы уже видели, на примере задач, решаемых за псевдополиномиальное время, представление чисел в "неэкономном" унарном коде переводит эти задачи из класса $$NPC \ (NP-ïîëíûõ)$$ в класс полиномиальных алгоритмов.
Однако, есть задачи, такие, что соответствующий им язык является -полным даже при представлении чисел в унарном коде!
Такие задачи -полны в сильном смысле.
продолжение следует...

[Pavlovsky]

Светлана, насколько я понял, вы сейчас тащательно изучаете класс NP-полных задач решаемых за псевдополиномиальное время. Где то можно почитать о результатах ваших трудов?

[Swetlana]

Валерий, это я сейчас для данной темы стараюсь, по принципу: назвался груздем - иди ... и изучай.
Вообще, как один мой знакомый говорит, "псевдополиномиальность задачи - это подарок судьбы".
Но у меня этот подарок судьбы возник только один раз, в задаче об отгрузке готовой листопрокатной продукции, причём для ММК в такой сверхбольшой размерности, к которой даже масштабированные алгоритмы динамического программирования не применимы.
А вообще этим много занимаются. Для коммивояжера с метрикой огромное количество англоязычных работ, PTAS всяких, на англоязычных форумах их обсуждают, питасами меряются

щас долблю путь коммивояжера без метрики, NP-полный в сильном смысле, новый алгоритм для него сочиняю. Полотпуска сидела, не поднимая головs, в сентябре из-за огромной учебной нагрузки забросила. Жутко тяжело идёт, потому что в программе нужно кешировать промежуточные вычисления, иначе медленно будет, никогда этого не делала раньше. Mbo и Pavia на сорцах советами помогали, летом, я рыдала, что не получается, они утешали
Не представляю, как сейчас открою программу, которую полгода назад забросила, на полуслове

[Swetlana]

Задачи с числовыми параметрами

нет, это не то, что вы подумали
Введём некоторые дополнительные определения

У нас уже есть независимая от схемы кодирования функция $$Length: \ D_Ï \rightarrow Z^+$$, длина входа для индивидуальной задачи .
Добавим ещё одну функцию, определяющую значение максимального целого числа задачи :
$$Max: \ D_Ï \rightarrow Z^+$$.
Если в задаче нет чисел (графы, элементы с именами и.т.д), то положим .
То есть каждой индивидуальной задаче , при некоторой разумной схеме кодирования, сопоставляются два целых положительных числа - длина входа и максимальное целое число, используемое в описании этой задачи.

Например, для индивидуальной задачи "Сумма размеров":

будем использовать десятичную систему счисления и звёздочки-разделители. Получаем входное слово: , , .
На самом деле мы могли закодировать набор данных по-другому, могли определить функцию по-другому, но все такие функции были бы полиномиально эквивалентны, если бы "по-другому" было бы разумной схемой . То есть можно считать, что функции $$Length\ è \ Max$$ не зависят от схемы кодирования.

Однако, дадим точное определение полиномиальной эквивалентности, на всякий случай
Определение 1. Две функции $$Length_1 \ è \ Length_2$$ для задачи распознавания $$Ï$$ полиномиально эквивалентны, если существуют такие полиномы $$p_1 \ è \ p_2$$, что для всех индивидуальных задач $$I \in D_Ï$$ выполнены следующие соотношения:
и .
от себя замечу, что очень похоже на эквивалентность различных норм, только константы заменены на полиномы

Определение 2. Пара функций для задачи распознавания $$Ï$$ полиномиально эквивалентна паре функций , если, во-первых, $$Length_1 \ è \ Length_2$$ эквивалентны в смысле Определения 1 и существуют такие полиномы от двух переменных $$q_1 \ è \ q_2$$, что для всех индивидуальных задач $$I \in D_Ï$$ выполнены следующие соотношения:
и .

Потребуем от функций $$Length \ è \ Max$$ выполнения ещё одного условия: они должны быть полиномиально вычислимы по коду индивидуальной задачи : существуют две ДМТ, которые, получив на вход код индивидуальной задачи $$I \in D_Ï$$, за полиномиальное время выдают на выход двоичные записи величин $$Length(I) \ è \ Max(I)$$.

Итак, чего мы добились. Для рассуждений на уровне языков нужно предъявлять схему кодирования. Рассуждая на уровне задач, мы оперируем двумя функциями $$Length \ è \ Max$$, полиномиально эквивалентными для всех разумных схем кодирования.

В качестве примера рассмотрим, как можно было бы выбрать функцию для задачи "Сумма размеров":
или .

Определение 3. Алгоритм решения задачи $$Ï$$ будет называться псевдополиномиальным по времени алгоритмом, если его временная функция сложности ограничена сверху полиномом от двух аргументов $$Length(I) \ è \ Max(I)$$.
Замечание 1. Так как полиномиальный алгоритм ограничен сверху полиномом от , то полиномиальный алгоритм есть частный случай псевдополиномиального.

Таким образом, - полная задача, в предположении, что , либо решается пседополиномиальным алгоритмом, либо не решается псевдополиномиальным алгоритмом, т.е. является - полной в сильном смысле.
Чтобы разобраться, для каких задач есть надежда найти псевдополиномиальный алгоритм, а какие заведомо - полны в сильном смысле, нам потребуется ещё одно определение.

Определение 4. Будем называть задачу $$Ï$$ задачей с числовыми параметрами, если не существует такого полинома , что для всех $$I \in D_Ï$$.

[Swetlana]

- полнота в сильном смысле

Какие задачи не являются задачами с числовыми параметрами?
Согласно Определению 4, задача с числовыми параметрами - это задача, в которой максимальное целое число ограничено сверху полиномом от длины входа для всех $$I \in D_Ï$$.
Во-первых, это задачи, в которых вообще нет чисел и , например, задача о существовании гамильтонова цикла в произвольном неориентированном графе.
Во-вторых, это задачи, где числа не превосходят числа объектов, заданных по условию задачи. Например, в задаче о максимальной клике (полном подграфе) спрашивается, существует ли в графе клика не менее, чем из вершин, где не превосходит числа вершин графа.
Для таких - полных задач найти псевдополиномиальный алгоритм -
всё равно что найти полиномиальный, что невозможно, в предположении, что .
Замечание 2. Если - полная задача $$Ï$$ не является задачей с числовыми параметрами, то $$Ï$$ не может быть решена псевдополиномиальным алгоритмом (если ).

Хочется написать ещё одно замечание, если задача $$Ï$$ является - полной и не является задачей с числовыми параметрами, то она автоматически - полна в сильном смысле. Но у нас пока нет определения задачи - полной в сильном смысле. :no:

Рассмотрим произвольную задачу распознавания $$Ï$$ и произвольный полином с целыми коэффициентами. Обозначим $$Ï_p$$ подзадачу, получаемую из $$Ï$$ рассмотрением только тех индивидуальных задач , для которых выполнено соотношение .
Подзадача $$Ï_p$$ не является задачей с числовыми параметрами. Если общая задача $$Ï$$ разрешима псевдополиномиальным алгоритмом , то подзадача $$Ï_p$$ будет разрешима за полиномиальное время, этим же алгоритмом .
Если же хотя бы одна такая подзадача будет - полной, т.е. не будет решаться полиномиальным алгоритмом, то и общая задача не будет решаться псевдополиномиальным алгоритмом.

Отсюда получаем следующее определение.
Определение 5. Задачу $$Ï$$ назовём - полной в сильном смысле, если $$Ï \in NP$$ и существует такой полином с целыми коэффициентами, что задача $$Ï_p$$ является - полной.

Вот теперь мы можем себе позволить
Замечание 3. Если задача $$Ï$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">NP$$ - полна и не является задачей с числовыми параметрами, то она автоматически является - полной в сильном смысле.
Замечание 4. Если задача $$Ï$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">NP$$ - полна в сильном смысле, то она не может быть решена псевдополиномиальным алгоритмом (если ).

Теперь мы должны привести пример задачи с числовыми параметрами, которая, однако, не разрешима за псевдополиномиальное время, с доказательством её сильной - полноты.

оставайтесь с нами...

[Swetlana]

Доказательство результатов о сильной - полноте

Вначале пойдём прямым путём и будем доказывать сильную - полноту просто по определению.
В качестве задачи $$Ï$$ с числовыми параметрами выберем задачу "Коммивояжер" (КМ). Действительно, это задача с числовыми параметрами, так как ни расстояния между городами, ни граница стоимости маршрута в ней не ограничены.

По определению сильной -полноты для какого-то конкретного полинома из КМ нужно выделить подзадачу такую, что для всех её индивидуальных подзадач верно:
и затем показать, что эта подзадача -полна.
Если бы исходная общая задача КМ решалась бы за пседополиномиальное время алгоритмом , то эта подзадача решалась бы за полиномиальное время. Раз она за полиномиальное время не решается ( - полная), значит, исходная задача не может решаться за псевдополиномиальное время, то есть - полна в сильном смысле.

Итак, где в КМ такая подзадача?
В посте №43 мы показали, что задача о существовании гамильтонова цикла (ГЦ) полиномиально сводится к задаче коммивояжера (КМ). Конкретно, мы показали, что - полной является подзадача КМ, в которой все расстояния между городами равны либо 1, либо 2, а граница стоимости маршрута равна числу городов.
В качестве полинома выбираем полином первой степени: .
Определим функцию длины входа задачи КМ как сумму числа городов, двоичного логарифма границы стоимости и суммы двоичных логарифмов расстояний между городами.
К слову, мы должны брать от логарифмов целую часть, длина входа - это целое число. Целую часть будем стандартно обозначать квадратными скобками.
, где - расстояние между городами и .
В качестве максимального целого числа можно взять максимум из границы и наибольшего расстояния между городами.
Тогда все полученные индивидуальные задачи будут:
1. удовлетворять условию ;
2. к ним, по уже доказанному, будет сводиться - полная задача о существовании гамильтонова цикла.
Значит, задача КМ - полна в сильном смысле.

Замечание. Почему при подсчёте длины входа количество городов берётся без логарифма, а граница стоимости и расстояния между городами - с логарифмами?
Потому что не числовой параметр, а количество объектов в нашей задаче, количество именованных вершин-городов, которые мы должны описать.

Итак, мы доказали сильную - полноту прямо по определению. Но настоящие герои всегда идут в обход! Настоящие герои:
1. вводят определение псевдополиномиальной сводимости; (Гэри-Джонсон, стр. 130)
2. доказывают лемму 4.1 стр. 131, о том, что псевдополиномиальная сводимость сохраняет сильную - полноту;
3. доказывают сильную - полноту посредством псевдополиномиальной сводимости.

Ты, мой неизвестный и удалённый читатель, и есть настоящий герой этого блога треда, тебе и Гэри-Джонсон в руки.

А я, учитывая пожелания модераторов, рассмотрю практические аспекты решения задач, разрешимых псевдополиномиальными алгоритмами, в случае разных размерностей, опираясь на свой небольшой опыт.
Выберем в качестве модельной задачу о наборе заданной суммы с помощью заданных слагаемых ("Сумма размеров") и будем решать её всеми способами для малой. средней, большой и сверхбольшой размерности.

[Swetlana]

Практические аспекты решения модельной задачи "Сумма размеров"

Вот постановка нашей модельной задачи:
"Сумма размеров"
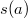
Условие. Заданы конечное множество $$À$$, целый положительный вес для каждого и целое положительное число .
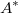
Вопрос. Существует ли в $$À$$ подмножество такое, что

А вот бухгалтер, милый мой бухгалтер, и у него есть не сильно много целых положительных чисел, , и ему нужно набрать заданную сумму , всеми возможными способами. Задача из класса .
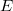
Раз , будем решать эту задачу алгоритмом с возвратом, с отсечением повторяющихся решений, с точностью до перестановок слагаемых внутри суммы. То есть решение выводим на печать, а решение не будем не только печатать, но и тратить время на его генерацию. Повторяющиеся решения мы не генерируем, что сильно ускорит выполнение программы, хотя алгоритм всё равно останется экспоненциальным.
Второй вопрос - велика ли сумма , которую нужно набрать. От ответа на этот вопрос зависит выбор структуры данных, в которой будут храниться слагаемые. Поскольку мне хочется продемонстрировать оригинальный способ хранения слагаемых, буду считать, что тоже невелико.

Задача о весах
Условие. Имеется разновес, причем гиря определенного веса может либо отсутствовать в разновесе, либо иметься в нескольких экземплярах. Задано целое положительное число - вес, который нужно набрать.
Вопрос. Набрать заданный вес всеми возможными способами с точностью до перестановки гирь.
Пример. Разновес: 8, 7, 3, 2, 2, 1, 1, 1. Набрать вес: 10кг.

Выбор структуры данных.
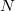
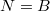
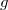
Разновес удобно хранить в массиве , где – либо вес самой тяжелой гири, либо и – количество экземпляров гири веса . То есть храним не сами гири, а количество штук каждого достоинства.
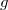
Решение (набор веса) будем хранить в массиве , где аналогично – количество экземпляров гири веса в текущем решении.

Первый подход к штанге весу
Применим обычную схему алгоритма с возвратом.
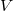
Пусть – текущий вес, который нужно набрать. Чтобы набрать этот вес, будем перебирать гири разновеса до тех пор, пока не встретим допустимую.
Условие допустимости гири:
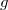
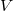
Гиря веса допустима, если она имеется в разновесе, то есть и ее вес не превышает набираемого веса , т.е..
Прямой ход
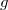
Пусть такая найдена, удалим ее из разновеса, то есть и добавим к решению, то есть . Новый текущий набираемый вес равен .
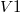
Если не равен 0, то вызываем рекурсию для дальнейшего набора веса, иначе печатаем решение.
Возврат:
Последнюю добавленную гирю удаляем из решения и добавляем в разновес:
.
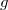
Затем возвращаемся на начало цикла перебора гирь и вместо гири веса берем гирю веса .
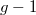
Увы, при таком способе перебора, будут генерироваться все перестановки слагаемых внутри суммы.

Генерация решения в лексикографическом порядке. Отсечение повторяющихся решений
Чтобы избавиться от повторов, будем генерировать решения в антиалфавитном порядке. Это означает следующее.
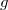
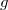
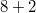
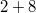
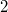
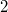
После того, как к решению была добавлена гиря веса , разрешается брать гири веса меньшего либо равного . Таким образом, будет сгенерировано только решение . Решение не генерируется, т.к. после можно брать либо (есть повторяющиеся гири), либо .
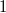
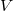
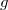
При вызове рекурсии для добора оставшегося веса будем передавать в качестве параметра не только вес (вес, который нужно набрать), но и - вес последней добавленной гири.

Код: Выбрать все

Алгоритм {задача о весах}
Данные: разновес, представленный массивом KRATN[1…Ves],
Ves – набираемый целый положительный вес.
Результат: печать наборов веса без перестановок гирь.
Переменные: Ves, KRATN, SOL – глобальные.
1 procedure nabor (V, g);
{V - набираемый вес, g - вес последней добавленной к решению гири}
2 begin {nabor}
3 for i = g downto 1 do
4 if (KRATN[i]>0) and (i<=V) then
5 begin
6 KRATN[i] = KRATN[i]-1;
7 SOL[i] = SOL[i]+1;
8 V1 = V-i;
9 if V1=0 then печать SOL
10 else nabor(V1, i);
{возврат}
11 KRATN[i] = KRATN[i]+1;
12 SOL[i] = SOL[i]-1;
13 end;
14 end; {nabor}

1 begin {main}
2 инициализация массива KRATN;
3 for j:=1 to Ves do SOL[j]:= 0;
4 nabor(Ves, Ves);
5 end.


Если нам устроит любое решение, то находим первое решение и выходим.

Программа была в Delphi, пришлось пришлось заменить ввод-вывод. Набираемый вес и вес min гири описаны константами, кратности гирь присваиваются прямо внутри программы, набор веса записывается в строку.
Если закомментировать строку STOP:=true; //найдено первое решение , то будут генерироваться все наборы веса.

Код: Выбрать все

program www;

 {$APPTYPE CONSOLE}

 uses
 SysUtils;

 const Ves=10;//набираемый вес
 MinV=1;//min вес гири
 var
 KRATN,SOL:array[MinV..Ves] of integer;
 k:integer;
 STOP:boolean; //найдено решение

 procedure nabor(g,v:integer);
 var
 i,j,kg:integer;
 s:string;
 begin
 if v=0 then
 begin //печать строки с набором суммы
 writeln('Summa:');
 s:='';
 for kg:=Ves downto 1 do
 for j:=1 to SOL[kg] do
 s:=s+'+'+IntToStr(kg);
 writeln(s);
 STOP:=true; //найдено первое решение
 end
 else if (v>0) AND NOT(STOP) then
 begin //добор веса
 for i:=g downto 1 do
 if (v>=i) and (kratn[i]>0) then
 begin
 kratn[i]:=kratn[i]-1;
 sol[i]:=sol[i]+1;
 nabor(i,v-i);
 kratn[i]:=kratn[i]+1;
 sol[i]:=sol[i]-1;
 end;
 end;
 end;

 begin
 for k:=MinV to Ves do
 begin
 KRATN[k]:=0; SOL[k]:=0;
 end;
 KRATN[8]:=1; KRATN[7]:=1; KRATN[3]:=1; KRATN[2]:=2; KRATN[1]:=3;
 STOP:=false; //решение не найдено
 nabor(Ves,Ves);
 readln;
 end.

[Swetlana]

Задачи распознавания и задачи оптимизации

Вся теория - полноты строится для задач распознавания.
Стандартная формулировка задачи распознавания $$(Ï)$$" title="$$: $$" align="middle" style="border: 0; vertical-align: middle">Äàíî \ À, \ âåðíî \ ëè \ ÷òî \ äëÿ \ À \ âûïîëíÿåòñÿ \ ñâîéñòâî \ Õ?$$
Решением такой задачи будем считать ответ "да" или "нет".

Как честный человек, должна сказать, что задача распознавания - частный случай переборной задачи, это определение вводится для труднорешаемых задач за пределами класса , так называемых - трудных задач, и для них определяется уже третий вид сводимости, сводимость по Тьюрингу (Гэри-Джонсон, глава 5).
Зачем, вот так, на ровном месте, к практическим аспектам вдруг приплести сводимость по Тьюрингу, тем более, что я собираюсь оставаться в пределах класса .

Дело в том, что кроме задач распознавания есть ещё задачи оптимизации, и 99% реальных производственных задач возникают именно как задачи оптимизации.
Каждую задачу оптимизации можно переформулировать как задачу распознавания, но не наоборот. То есть некоторые задачи существуют в виде пары "распознавание - оптимизация".
Например, задача ГЦ о существовании гамильтонова цикла в произвольном неориентированном графе не имеет оптимизационной пары, цикл либо есть, либо нет.

А задача КМ (коммивояжер) может быть сформулирована либо как задача распознавания:
Условие. Имеется городов, известны целые положительные расстояния между каждой парой городов. Задано целое положительное число $$Â$$.
Вопрос. Существует ли гамильтонов цикл стоимостью меньше либо равной $$Â$$?
либо как задача оптимизации:
Условие. Имеется городов, известны целые положительные расстояния между каждой парой городов.
Вопрос. Найти гамильтонов цикл минимальной стоимости.

Простой приём - вводится граница стоимости , в задаче минимизации ищем объект стоимости не превосходящей , в максимизации - стоимости больше . Но.
Мы построили всю теорию - полноты для задач распознавания, для задач оптимизации автоматически ничего не следует. Нужно доказывать снова да ладом.
Без доказательства, по Гэри-Джонсону, глава 5, стр. 147.

...Если рассмотреть пару задач, одна из которых - задача распознавания (ЗР), а другая - соответствующая оптимизационная задача (ОЗ), то ЗР сводима по Тьюрингу к ОЗ, и ОЗ сводима по Тьюрингу к ЗР.
Таким образом, каждая задача из пары ЗР - ОЗ может быть решена за полиномиальное время тогда и только тогда, когда другая задача полиномиально разрешима.
Поскольку задача распознавания является - полной, именно для задач распознавания мы построили всю теорию - полноты, то отсюда следует, что соответствующая оптимизационная задача может быть решена за полиномиальное время в одном единственном случае: если .

Теперь рассмотрим задачу "Сумма размеров": заданы набор целых положительных слагаемых и число , спрашивается, существует ли набор числа с помощью заданных слагаемых.

Внимание, вопрос: Есть ли у задачи "Сумма размеров" оптимизационная пара?

[Sonic86]

Source of the post Каждую задачу оптимизации можно переформулировать как задачу распознавания, но не наоборот. То есть некоторые задачи существуют в виде пары "распознавание - оптимизация".
Например, задача ГЦ о существовании гамильтонова цикла в произвольном неориентированном графе не имеет оптимизационной пары, цикл либо есть, либо нет.

Это почему это? :blink: Нам на лекциях давали равносильность этих задач. Задача ГЦ в виде оптимизации - вроде та же задача с ЦФ = числу ребер ГЦ + условие "число ребер = числу вершун". Просто значение ЦФ на всех циклах равно константе. Ну и ладно. Ничего страшного.

[Swetlana]

Source of the post

Source of the post Каждую задачу оптимизации можно переформулировать как задачу распознавания, но не наоборот. То есть некоторые задачи существуют в виде пары "распознавание - оптимизация".
Например, задача ГЦ о существовании гамильтонова цикла в произвольном неориентированном графе не имеет оптимизационной пары, цикл либо есть, либо нет.

Это почему это? :blink: Нам на лекциях давали равносильность этих задач. Задача ГЦ в виде оптимизации - вроде та же задача с ЦФ = числу ребер ГЦ + условие "число ребер = числу вершун". Просто значение ЦФ на всех циклах равно константе. Ну и ладно. Ничего страшного.

ага, интересно, давайте разбираться
с точки зрения математического программирования, оптимизация бывает условной или безусловной, в принципе, нам тут без разницы
далее, целевая функция либо максимизируется, либо минимизируется
но не равна константе
иначе набор заданного веса B превращается в оптимизацию
а какая тогда у него будет задача распознавания?