НДМТ и алгоритмы с возвратомНДМТ не только модель абстрактного вычислителя. Это ещё и способ организовать переборный алгоритм, даже если у нас нет возможности организовать параллельные независимые вычисления.
Алгоритм с возвратом (backtracking)Рассмотрим общую схему алгоритма с возвратом на примере задачи поиска всех гамильтоновых циклов в неориентированном графе

. Каждый такой цикл – последовательность различных вершин графа

и только

, где
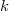
– произвольная фиксированная вершина, соседние вершины
$$X(i) \ è \ X(i+1)$$ соединены ребром.
Вначале произведём
полный перебор всех возможных путей.
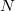
вершин графа можно расположить в
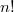
различных цепочек. Чтобы проверить для каждой цепочки, реализована ли она как гамильтонов путь на графе, необходимо еще

шагов, итого сложность полного перебора
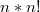
шагов.
Такая величина растет гораздо быстрее экспоненты, однако число шагов в алгоритмах переборного типа можно значительно уменьшить, оставаясь, разумеется, в классе экспоненциальных алгоритмов.
ОБЩАЯ СХЕМА АЛГОРИТМА С ВОЗВРАТОМПроще всего алгоритм с возвратом записать с помощью рекурсии, однако, для порядка, рассмотрим вначале нерекурсивный вариант.
Пусть решение, которое мы ищем, имеет вид последовательности
$$\langle X(1),
, X(n) \rangle$$ .
Будем строить его, начиная с пустой последовательности длины
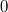
.
Пусть на каком-то этапе уже построено частичное (неполное) решение длины
$$i: \langle X(1),
, X(i) \rangle$$.
Попытаемся продолжить это решение ещё на один шаг. Для этого нужно отыскать допустимое
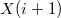
.
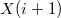
считается допустимым, если или
$$\langle X(1),
, X(i+1) \rangle$$ уже является решением, или относительно
$$\langle X(1),
, X(i+1) \rangle$$ нельзя сразу сказать, что это тупик, который невозможно расширить до полного решения.
Далее существует две возможности:
– если
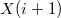
допустимо, то следующее допустимое
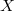
ищется для частичного решения
$$\langle X(1),
, X(i+1) \rangle$$;
(заметим, что допустимость
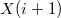
вовсе не означает, что
$$\langle X(1),
, X(i+1) \rangle$$ можно расширить до полного решения)
– если допустимого
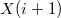
не существует, то возвращаемся на шаг назад – к частичному решению
$$\langle X(1),
, X(i-1) \rangle$$ и для него отыскиваем другое

, не совпадающее с предыдущим
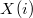
.
Более точно, пусть для каждого
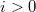
существует множество
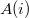
, из которого будут выбираться
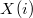
– претенденты на
$$i$$ю координату частичного решения. Очевидно, множества
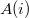
должны содержать все
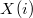
, занимающие
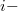
ю координату любого решения. Кроме того,
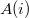
будут содержать какие-то лишние элементы, не содержащие в
$$i$$й координате ни одного решения.
Теперь нерекурсивная схема алгоритма с возвратом имеет следующий вид:
Код: Выбрать все
1 begin
2 k:= 1;
3 while k>0 do
4 if существует еще новый y из A(k), являющийся допустимым then
5 begin
6 X[k]:= y;
7 y использован;
8 if <X[1],…,X[k]> является решением then write (<X[1],…,X[k]>);
9 k:= k+1;
10 end
11 else {возврат на предыдущее частичное решение, все элементы A(k) становятся новыми}
12 k:= k-1
13 end.Если все решения имеют длину, меньшую
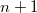
, и все множества
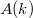
состоят из конечного числа элементов, то этот алгоритм находит все возможные решения.
Тот же самый алгоритм можно очень просто записать с помощью рекурсии.
Рекурсивный вариант алгоритма с возвратом Код: Выбрать все
1 procedure BC(k);
{генерируем все решения, являющиеся продолжением частичного решения <X[1],…,X[k-1]>,
массив Х– глобальный}
2 begin
3 for y из A(k) do
4 if y допустим then
5 begin
6 X[k]:= y;
7 if <X[1],…,X[k]> – решение then write(<X[1],…,X[k]>);
8 BC(k+1); // генерируем все решения, являющиеся продолжением
// частичного решения <X[1],…,X[k-1],y>}
// возврат
9 y новый; //возврат на <X[1],…,X[k-1]>
10 end // возврат на цикл 3
11 end;