Интегральные уравнения

da67 · Сообщение **da67** » 04 июл 2012, 15:31

Вы знакомы с дельта-функцией? Допустимо ли для вас равенство $|x|''=2\delta(x)$ ?
Если да, то всё просто. Если нет, придётся помучаться.

inferno1993 · Сообщение **inferno1993** » 04 июл 2012, 15:43

da67 писал(а):Source of the post
Вы знакомы с дельта-функцией? Допустимо ли для вас равенство $|x|''=2\delta(x)$ ?
Если да, то всё просто. Если нет, придётся помучаться.

нет, не знаком. И как то не вяжется мое уравнение с этим равенством помоему

da67 · Сообщение **da67** » 04 июл 2012, 16:16

Тогда придётся по-старинке.
Нужно найти вторую производную функции
$\displaystyle f(s)=\int_{0}^{\pi/2}K(s,t)\,x(t)\,dt =0$
С первой просто: т.к. $$K$$

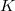непрерывна, получим
$\displaystyle f'(s)=\int_{0}^{\pi/2}L(s,t)\,x(t)\,dt =0$
где $L(s,t)=\frac{\partial K(s,t)}{\partial s}$ -- разрывная при $$s=t$$

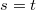функция.
Теперь аккуратно рассмотрите разность итегралов при двух близких значениях $$s$$

. При $t\ne s$ получится просто производная ядра, как и раньше, а от места разрыва возникнет дополнительный член. Ваша задача его поймать.

inferno1993 · Сообщение **inferno1993** » 04 июл 2012, 16:25

da67 писал(а):Source of the post
Тогда придётся по-старинке.
Нужно найти вторую производную функции
$\displaystyle f(s)=\int_{0}^{\pi/2}K(s,t)\,x(t)\,dt =0$
С первой просто: т.к. непрерывна, получим
$\displaystyle f'(s)=\int_{0}^{\pi/2}L(s,t)\,x(t)\,dt =0$
где $L(s,t)=\frac{\partial K(s,t)}{\partial s}$ -- разрывная при функция.
Теперь аккуратно рассмотрите разность итегралов при двух близких значениях . При $t\ne s$ получится просто производная ядра, как и раньше, а от места разрыва возникнет дополнительный член. Ваша задача его поймать.

Да, я с этим практически разобрался, просто после производной я нашел общее решение и не мог понять как из него найти собственные значения и характеристические функции. Потом понял, что нужно подобрать такие лямбда, чтобы уравнение имело нетривиальное решение. поэтому лямбда получилось 4n^2 -1.
Спасибо за подсказку.

da67 · Сообщение **da67** » 04 июл 2012, 16:26

Единичка как раз и вылезает из-за разрыва.

inferno1993 · Сообщение **inferno1993** » 04 июл 2012, 16:30

Понятно, из-за него в диф уравнении просто и вылезает x(s) без коэффициента лямбда.

yourdomain.com