Доказать, что..
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Доказать, что..
Пусть 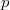 - простое число, большее 3 и
- простое число, большее 3 и ![$$k=\left[\frac{2p}{3}\right]$$ $$k=\left[\frac{2p}{3}\right]$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24k%3D%5Cleft%5B%5Cfrac%7B2p%7D%7B3%7D%5Cright%5D%24%24) . Доказать, что
. Доказать, что 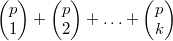 делится на
делится на 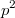
Последний раз редактировалось JeffLebovski 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Доказать, что..
Интересно, а в кольце 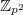 эта сумма свернётся?
эта сумма свернётся?
Последний раз редактировалось JeffLebovski 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
-
Forest1333
- Сообщений: 23
- Зарегистрирован: 04 дек 2009, 21:00
Доказать, что..
Что-то я понять не могу... В скобках дроби стоят?
Последний раз редактировалось Forest1333 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Доказать, что..
Нет, а с чего бы им там стоять?
Так как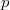 - простое, тое
- простое, тое  - целое. Тогда надо доказать, что
- целое. Тогда надо доказать, что  делится на
делится на 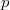 .
.
Дальше не продвинулся....
Так как
Дальше не продвинулся....
Последний раз редактировалось JeffLebovski 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать, что..
Что-то я понять не могу... В скобках дроби стоят?
Так обозначаются биномиальные коэффициенты:
Последний раз редактировалось Sonic86 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать, что..
JeffLebovski писал(а):Source of the post
Нет, а с чего бы им там стоять?
Так как- простое, тое
- целое. Тогда надо доказать, что
делится на
.
Дальше не продвинулся....
Че-то как-то неправильно Вы преобразовали сумму (проверьте сами формально подстановкой
Можно преобразовать и так:
Толку тоже мало. Странное очень значение
Вообще, сумма, как известно, в замкнутом виде не вычисляется (см. Конкретную математику, с.191). Смог преобразовать к виду:
Тоже не помогает
[url=http://dxdy.ru/topic47956.html]http://dxdy.ru/topic47956.html[/url]
Последний раз редактировалось Sonic86 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Доказать, что..
Sonic86, правильно ли я понял вот это переход:
Рассмотрим . В поле
. В поле 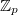 имеем
имеем  .
.
Т.е. надо доказать, что в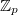
![$$\sum\limits_{1\leqslant j\leqslant\left[\frac12\left[\frac{2p}{3}\right]\right]}\frac1{j}+\sum\limits_{j>\left[\frac{2p}{3}\right]}\frac1{j}=0$$ $$\sum\limits_{1\leqslant j\leqslant\left[\frac12\left[\frac{2p}{3}\right]\right]}\frac1{j}+\sum\limits_{j>\left[\frac{2p}{3}\right]}\frac1{j}=0$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Csum%5Climits_%7B1%5Cleqslant%20j%5Cleqslant%5Cleft%5B%5Cfrac12%5Cleft%5B%5Cfrac%7B2p%7D%7B3%7D%5Cright%5D%5Cright%5D%7D%5Cfrac1%7Bj%7D%2B%5Csum%5Climits_%7Bj%3E%5Cleft%5B%5Cfrac%7B2p%7D%7B3%7D%5Cright%5D%7D%5Cfrac1%7Bj%7D%3D0%24%24) . Понятно, что
. Понятно, что 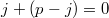 . Как Вы доказали, что при
. Как Вы доказали, что при ![$$k=\left[\frac{2p}{3}\right]}$$ $$k=\left[\frac{2p}{3}\right]}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24k%3D%5Cleft%5B%5Cfrac%7B2p%7D%7B3%7D%5Cright%5D%7D%24%24) они все поуничтожаются?
они все поуничтожаются?
Рассмотрим
Т.е. надо доказать, что в
Последний раз редактировалось JeffLebovski 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать, что..
JeffLebovski писал(а):Source of the post
Sonic86, правильно ли я понял вот это переход:
Рассмотрим. В поле
имеем
.
Жесть! Можно так:
JeffLebovski писал(а):Source of the post
И ещё я не могу понять, как Вы после сложенияи
одно из слагаемых получили
Поясниет пожалуйста.
Сначала я из суммы \sum\limits_{j=1}^{p-1}\frac1j выделил кусок с
Последний раз редактировалось Sonic86 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Доказать, что..
Ваши две последние строчки в решении, я так понял, что в 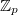
![$$\left[\frac{[\frac{2p}{3}]}{2}\right]+[\frac{2p}{3}]+1=0$$ $$\left[\frac{[\frac{2p}{3}]}{2}\right]+[\frac{2p}{3}]+1=0$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Cleft%5B%5Cfrac%7B%5B%5Cfrac%7B2p%7D%7B3%7D%5D%7D%7B2%7D%5Cright%5D%2B%5B%5Cfrac%7B2p%7D%7B3%7D%5D%2B1%3D0%24%24) . Проверил для нескольких первых простых, действительно так. А как Вы это показали для произвольного
. Проверил для нескольких первых простых, действительно так. А как Вы это показали для произвольного 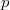 ?
?
Последний раз редактировалось JeffLebovski 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать, что..
JeffLebovski писал(а):Source of the post
Ваши две последние строчки в решении, я так понял, что в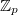
. Проверил для нескольких первых простых, действительно так. А как Вы это показали для произвольного
?
Я, если честно, это не проверил
Вообще, простые числа
Последний раз редактировалось Sonic86 28 ноя 2019, 20:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 5 гостей