Как вычислить два последних интеграла я незнаю, подскажите пожалуйста
ЛНДУ второго порядка
ЛНДУ второго порядка
Здраствуйте уважаемые Математики! Если у Вас есть немного помоите разобраться.





















Как вычислить два последних интеграла я незнаю, подскажите пожалуйста
Как вычислить два последних интеграла я незнаю, подскажите пожалуйста
Последний раз редактировалось Бзяка 28 ноя 2019, 20:53, всего редактировалось 1 раз.
Причина: test
Причина: test
ЛНДУ второго порядка
Поправил.Бзяка писал(а):Source of the post
Здраствуйте уважаемые Математики! Если у Вас есть немного помоите разобраться.
Теперь интегралы берущиеся
Последний раз редактировалось СергейП 28 ноя 2019, 20:53, всего редактировалось 1 раз.
Причина: test
Причина: test
ЛНДУ второго порядка
Интеграл от любой рациональной функции от 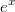 можно найти заменой
можно найти заменой 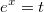 .
.
Последний раз редактировалось bas0514 28 ноя 2019, 20:53, всего редактировалось 1 раз.
Причина: test
Причина: test
ЛНДУ второго порядка
Спасибо, Вам, за исправления и советы.
Я только не понял, как у Вас получилось дельта таким и если проводить замену ex=t, то e-x=1/t e-2x=1/t2, а dx=dt ?
Я только не понял, как у Вас получилось дельта таким и если проводить замену ex=t, то e-x=1/t e-2x=1/t2, а dx=dt ?
Последний раз редактировалось Бзяка 28 ноя 2019, 20:53, всего редактировалось 1 раз.
Причина: test
Причина: test
ЛНДУ второго порядка
Да.
Последний раз редактировалось bas0514 28 ноя 2019, 20:53, всего редактировалось 1 раз.
Причина: test
Причина: test
ЛНДУ второго порядка
Спасибо Вам еще раз, Б.А.С.
Последний раз редактировалось Бзяка 28 ноя 2019, 20:53, всего редактировалось 1 раз.
Причина: test
Причина: test
ЛНДУ второго порядка
Последний раз редактировалось СергейП 28 ноя 2019, 20:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 28 гостей