Существует ли такое множество
Наименьший простой делитель
Наименьший простой делитель
Оцените, пожалуйста, красоту данной задачи. Я знаю, что решение простое (если даже я за 15 минут решила :lool: ), но условие, на мой взгляд, очень красивое.
Существует ли такое множество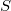 из 4020 натуральных чисел, что наименьший простой делитель суммы элементов любого 2011-элементного подмножества
из 4020 натуральных чисел, что наименьший простой делитель суммы элементов любого 2011-элементного подмножества 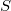 превышает 2011?
превышает 2011?
Существует ли такое множество
Последний раз редактировалось Xenia1996 29 ноя 2019, 08:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Наименьший простой делитель
A если так:Xenia1996 писал(а):Source of the post
Существует ли такое множествоиз 4020 натуральных чисел, что наименьший простой делитель суммы элементов любого 2011-элементного подмножества
превышает 2011?
Существует ли такое множество
Какая разница в решении : Про каждое простое число <2011 (и все их вместе этого можно добиться. Пусть нащлись
Зато если есть пример для более слабого требования, он заведомо проще, можно вообще работать c 4020 числами из набора (0,1,..2010)
Я как-то и не стремился до конца вперед других решать, но напомнило интересную, и не полностью обсужденную
Последний раз редактировалось Ian 29 ноя 2019, 08:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Наименьший простой делитель
Ian писал(а):Source of the postA если так:Xenia1996 писал(а):Source of the post
Существует ли такое множествоиз 4020 натуральных чисел, что наименьший простой делитель суммы элементов любого 2011-элементного подмножества
превышает 2011?
Существует ли такое множествоиз 4020 натуральных чисел, что ни один простой делитель суммы элементов любого 2011-элементного подмножества
не равен 2011?
Какая разница в решении : Про каждое простое число <2011 (и все их вместе этого можно добиться. Пусть нащлисьдля второй формулировки, нас интересуют только остатки их от деления на 2011.Тогда их можно подправить c сохранением у каждого остатка на 2011, но чтоб остаток на 2010! у каждого был равен 1, то есть удовлетворив более слабое требование, удовлетворим и более сильное.
Зато если есть пример для более слабого требования, он заведомо проще, можно вообще работать c 4020 числами из набора (0,1,..2010)
Я как-то и не стремился до конца вперед других решать, но напомнило интересную, и не полностью обсужденную
Я имела в виду взять 2010 чисел, делящихся на 2011, но дарамдаш остаток 1 на все простые, которые меньше 2011, и 2010 чисел, дарамдаш остаток 1 на все простые, не превышающие 2011.
Ho задача по Вашей ссылке, конечно, интереснее.
Последний раз редактировалось Xenia1996 29 ноя 2019, 08:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Наименьший простой делитель
Ian писал(а):Source of the postA если так:Xenia1996 писал(а):Source of the post
Существует ли такое множествоиз 4020 натуральных чисел, что наименьший простой делитель суммы элементов любого 2011-элементного подмножества
превышает 2011?
Существует ли такое множествоиз 4020 натуральных чисел, что ни один простой делитель суммы элементов любого 2011-элементного подмножества
не равен 2011?
Какая разница в решении : Про каждое простое число <2011 (и все их вместе этого можно добиться. Пусть нащлисьдля второй формулировки, нас интересуют только остатки их от деления на 2011.Тогда их можно подправить c сохранением у каждого остатка на 2011, но чтоб остаток на 2010! у каждого был равен 1, то есть удовлетворив более слабое требование, удовлетворим и более сильное.
Зато если есть пример для более слабого требования, он заведомо проще, можно вообще работать c 4020 числами из набора (0,1,..2010)
Я как-то и не стремился до конца вперед других решать, но напомнило интересную, и не полностью обсужденную
Ian, я никак не могу взять в толк, почему Вы решили другую задачу. У Bac сумма не делится на 2011, a у Xenia1996 - ни на одно простое число
Вашу же задачу можно тоже решить способом Xenia1996 - взять 2010 чисел 0 по модулю 2011, и еще 2010 чисел 1 по модулю 2011.
Последний раз редактировалось typhoon 29 ноя 2019, 08:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Наименьший простой делитель
Потому что эквивалентныtyphoon писал(а):Source of the post
Ian, я никак не могу взять в толк, почему Вы решили другую задачу.
Да.Например, 2010 единиц и 2010 чисел 2011 A из этого набора,как и из любого, решающего мою задачу, я собирался построить набор, в котором остатки от деления на 2011 такие же, a все остатки от деления на все простые p<2011 равны 1. Это возможно по китайской теореме об остатках.Получается ровно то же, что Ксения придумала. И фактически она тоже пользовалась китайской теоремой, явно же не привела числа.Это могли бы быть 2010 единиц и 2010 равных чиселУ Bac сумма не делится на 2011, a у Xenia1996 - ни на одно простое число.
Вашу же задачу можно тоже решить способом Xenia1996 - взять 2010 чисел 0 по модулю 2011, и еще 2010 чисел 1 по модулю 2011.
Последний раз редактировалось Ian 29 ноя 2019, 08:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 18 гостей