A1. Пусть

- действительные числа открытого интервала
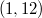
. Докажите, что существуют различные
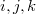
такие, что
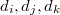
являются длинами сторон остроугольного треугольника.
A2. Пусть

- коммутативная ассоциативная бинарная операция на множестве
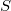
. Предположим, что для всех

существует

такое, что
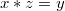
. Докажите, что если
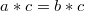
, то
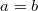
.
A3. Пусть
![$$f:[-1,1]\to\mathbb{R}$$ $$f:[-1,1]\to\mathbb{R}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24f%3A%5B-1%2C1%5D%5Cto%5Cmathbb%7BR%7D%24%24)
- непрерывная, такая что:
(i)
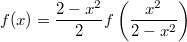
(ii)
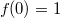
(iii)

- существует и конечен.
Докажите, что такая
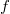
- единственна и найдите ее.
A4. Пусть
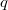
и

- целые числа, причем
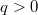
и пусть
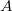
и

- интервалы на числовой прямой. Пусть
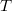
- мнжество всех чисел вида
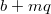
, где

и

- целые чила, такие что

, а
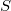
- множество всех целых

, Таких что

. Показать, что если произведение длин
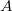
и

меньше, чем
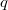
, то
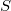
является пересечением
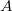
с некоторой арифметической прогрессией.
A5. Пусть
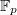
означает поле целых чисел по модулю простого числа
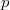
и пусть

- некоторое натуральное число. Пусть

- фиксированный вектор, принадлежащий
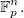
Пусть
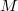
- матрица

с элементами из
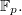
Определим отображение

формулой
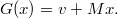
Пусть
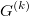
обозначает
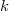
-кратную композицию отображения
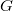
с самим собой, то есть
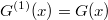
и
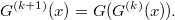
Найдите все пары
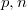
для которых существуют

и
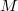
, такие что все
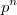
векторов
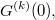
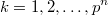
попарно различны.
A6. Пусть
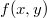
- непрерывная вещественнозначная функция на
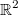
. Предположим, что на каждой прямоугольной области площади 1 двойной интеграл от
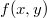
по этой области равен 0. Следует ли отсююда, что

?
B1. Обозначим через
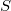
- класс функций

, удовлетворяющих следующим условиям:
(i)
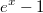
и

принадлежат
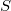
(ii) Если

, то

(iii) Если

для всех

, то

.
Докажите, что если

, то

.
B4. Пусть
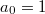
и
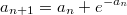
. Сущствует ли предел последовательности

?
P.S. Листок с чатью

Где-то потерял. Если найду, выложу...
- класс функций, определенных на
со значениями в
, удовлетворяющий условиям:
и
принадлежат
и
принадлежат
то
и
тоже принадлежат
принадлежат
и
для всех
то функция
принадлежит
и
принадлежат
то функция
тоже принадлежит