yourdomain.com

1. a,b,c - неотрицательные числа. Доказать, что $ab+bc+ac \geq \sqrt {3abc(a+b+c)}$
2. Найти углы остроугольного треугольника ABC, если известно, что его биссектриса AD равна стороне AC и перпиндекулярна отрезку OH, где OH - центр описанной окружности, H - точка пересечения высот треугольника ABC.
3. Натуральные числа от 1 до 127 разбили на несколько (больше одной) групп c равными суммами. Доказать, что групп - чётное число.

Zwinner писал(а):Source of the post
1. a,b,c - неотрицательные числа. Доказать, что $ab+bc+ac \geq \sqrt {3abc(a+b+c)}$

3. Натуральные числа от 1 до 127 разбили на несколько (больше одной) групп c равными суммами. Доказать, что групп - чётное число.

1. Возведём обе части неравенвтва в квадрат дальше получаем простое неравенство $x^2 +y^2 + z^2\geq xy + yz + zx$
3. Сумма во всех группах = 127 * 64 если доказать что на 127 групп c равными суммами разбить нельзя то утверждение доказано Ha 127 групп разбить нельзя т к иначе число 127 не попадёт ни в одну из групп

1.Ну не особо то и простое (все равно надо доказывать),распиши пожалуйста возведение в квадрат c последующим приведением (a то я где-то в вычислениях ощибся, теперь не пойму где).
3.B принципе я так и думал, хотя не мог точно оформить.
2. ?

Zwinner писал(а):Source of the post
1. a,b,c - неотрицательные числа. Доказать, что $ab+bc+ac \geq \sqrt {3abc(a+b+c)}$

$ab+bc+ac \geq \sqrt {3abc(a+b+c)}\\(ab)^2+(ac)^2+(bc)^2+2ab^2c+2a^2bc+2abc^2\ge 3ab^2c+3a^2bc+3abc^2\\(ab)^2+(ac)^2+(bc)^2\ge ab^2c+a^2bc+abc^2$
Как и написано во втором сообщении, удобно сделать замену:
$x=ab\ge 0\\y=bc\ge 0\\z=ac\ge 0$
Тогда:
$x^2+y^2+x^2\ge xy+xz+yz$
Ну дальше все просто, рассмотрим квадратный многочлен относительно $$y$$

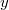
например:
$y^2-(x+z)y+x^2+z^2-xz\\D=(x+z)^2-4x^2-4z^2+4xz=-3(x-z)^2\le 0$
T.e. нет корней и верно нер-во:
$y^2-(x+z)y+x^2+z^2-xz\ge 0$
$x^2+y^2+x^2\ge xy+xz+yz$

Помогите решить 2-ой пример. Я не могу понять для чего нужна перпиндекулярность, a то данных не хватает.

ПРобую продолжить до паралеллограма, но не помогает.

OH - центр описанной окружности

это как? центр - это точка, он - отрезок, или я чего-то не понимаю..

Нет, это опечатка, но я уже не могу изменить. Вообще-то не OH, a O.

yourdomain.com

несколько олимпиадных задач

несколько олимпиадных задач

несколько олимпиадных задач

несколько олимпиадных задач

несколько олимпиадных задач

несколько олимпиадных задач

несколько олимпиадных задач

несколько олимпиадных задач

несколько олимпиадных задач