Задача о порядочных беспорядках
- buratino.2016
- Сообщений: 273
- Зарегистрирован: 07 сен 2015, 21:00
Задача о порядочных беспорядках
Пусть имеем порядок: 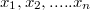 и один из его беспорядков. Представим, что порядок и беспорядок - это два различных порядка. Необходимо найти количество беспорядков, являющихся беспорядками обеих этих порядков.
и один из его беспорядков. Представим, что порядок и беспорядок - это два различных порядка. Необходимо найти количество беспорядков, являющихся беспорядками обеих этих порядков.
Последний раз редактировалось buratino.2016 27 ноя 2019, 18:02, всего редактировалось 1 раз.
Причина: test
Причина: test
- buratino.2016
- Сообщений: 273
- Зарегистрирован: 07 сен 2015, 21:00
Задача о порядочных беспорядках
Ищем беспорядки к первому порядку, затем ко второму. Пересечение этих множеств дает беспорядки, принадлежащие обеим порядкам. Но нам необходимо вывести(подобрать, получить) обобщенную формулу для количества этих беспорядков при различных n.
Последний раз редактировалось buratino.2016 27 ноя 2019, 18:02, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о порядочных беспорядках
Последний раз редактировалось grigoriy 27 ноя 2019, 18:02, всего редактировалось 1 раз.
Причина: test
Причина: test
- buratino.2016
- Сообщений: 273
- Зарегистрирован: 07 сен 2015, 21:00
Задача о порядочных беспорядках
Не, это было бы слишком просто.
Всего перестановок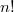
Если одну перестановку принять за порядок, то у этого порядка будет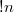 (субфакториал n) беспорядков, что равно ближайшему целому к
(субфакториал n) беспорядков, что равно ближайшему целому к 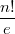 .
.
А если мы возьмем в качестве порядка исходный порядок и один из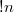 беспорядков, то необходимо найти такие беспорядки, которые будут являтся беспорядками для обоих этих порядков. Можно условно назвать их "двойными беспорядками".
беспорядков, то необходимо найти такие беспорядки, которые будут являтся беспорядками для обоих этих порядков. Можно условно назвать их "двойными беспорядками".
Под беспорядком понимается: https://ru.wikipedia.org/wiki/Беспорядок_(перестановка)
Возможно даже, что задача нерешаема или имеет в качестве решения многозначную функцию. Уже для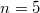 количество двойных беспорядков зависит от выбора порядков. Т.е. пары порядков распределяются на 2 вида. для одних из них существует 12 двойных беспорядков, для других- 13.
количество двойных беспорядков зависит от выбора порядков. Т.е. пары порядков распределяются на 2 вида. для одних из них существует 12 двойных беспорядков, для других- 13.
Всего перестановок
Если одну перестановку принять за порядок, то у этого порядка будет
А если мы возьмем в качестве порядка исходный порядок и один из
Под беспорядком понимается: https://ru.wikipedia.org/wiki/Беспорядок_(перестановка)
Возможно даже, что задача нерешаема или имеет в качестве решения многозначную функцию. Уже для
Последний раз редактировалось buratino.2016 27 ноя 2019, 18:02, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о порядочных беспорядках
О беспорядках впервые слышу. Думал Вы так называете перестановки.
Муторная задачка. Хотя кому-то и интересна и может где-то даже и важна...
Муторная задачка. Хотя кому-то и интересна и может где-то даже и важна...
Последний раз редактировалось grigoriy 27 ноя 2019, 18:02, всего редактировалось 1 раз.
Причина: test
Причина: test
- buratino.2016
- Сообщений: 273
- Зарегистрирован: 07 сен 2015, 21:00
Задача о порядочных беспорядках
Да , перспективы в решении этой задачки похоже не радужные. И это только добавляет ей муторности и интересности
Последний раз редактировалось buratino.2016 27 ноя 2019, 18:02, всего редактировалось 1 раз.
Причина: test
Причина: test
- buratino.2016
- Сообщений: 273
- Зарегистрирован: 07 сен 2015, 21:00
Задача о порядочных беспорядках
Пусть есть порядок и один из его беспорядков. Запишем их друг под другом и рассмотрим следующие рассуждения:
Мы имеем таблицу из 2-х строк и n столбцов, в столбцах которой нет ни одного дубля. Третью строку мы можем записать n! числом способов. Если из этих n! способов вычесть количество тех, при которых в столбцах таблицы возникнет 1 дубль, 2 дубля,3 дубля,......, n дублей, то останутся те способы, заполнения третьей строки, при которых в таблице не будет ни дублей, ни триплетов. Они и будут беспорядками порядков, представленных в первых двух строках.
при заполнении третьей строки один дубль может возникнуть на любой из n ячеек строки. Т.е. может возникнуть на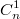 местах, при этом совпадение значения третьей строки в столбце может быть как с первой, так и со второй строкой, т.е. количество вариантов одного дубля удваивается. Все остальные
местах, при этом совпадение значения третьей строки в столбце может быть как с первой, так и со второй строкой, т.е. количество вариантов одного дубля удваивается. Все остальные 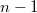 ячейки строки могут быть заполнены
ячейки строки могут быть заполнены 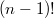 способами, в которых кстати также могут быть и дубли. Таким образом, Количество заполнений третьей строки в которых присутствует хотябы один дубль равно
способами, в которых кстати также могут быть и дубли. Таким образом, Количество заполнений третьей строки в которых присутствует хотябы один дубль равно 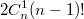 , но нам необходимо было вычесть из n! количество комбинаций, содержащих ровно один дубль, а не хотябы один. Получается, что мы вычли лишнее: комбинации, содержащие более одного дубля. Поэтому прибавим комбинации, включающие хотябы два дубля. Их количество будет
, но нам необходимо было вычесть из n! количество комбинаций, содержащих ровно один дубль, а не хотябы один. Получается, что мы вычли лишнее: комбинации, содержащие более одного дубля. Поэтому прибавим комбинации, включающие хотябы два дубля. Их количество будет 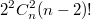 , пользуясь методом включения-исключения доберемся до последнего слагаемого: (-1)^n2^nC_n^n(n-n)! и общая формула примет вид:
, пользуясь методом включения-исключения доберемся до последнего слагаемого: (-1)^n2^nC_n^n(n-n)! и общая формула примет вид:
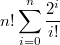 и при достаточно больших n выражение примерно равно
и при достаточно больших n выражение примерно равно 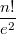
Вроде бы рассуждения верные, но компьютерный расчет опровергает этот результат. На самом деле решение раздваивается и зависит не только от n, но и от выбора первых двух строк. Из-за чего может происходить такое раздвоение результатов? Какие ошибки могут быть в приведенных рассуждениях?
Мы имеем таблицу из 2-х строк и n столбцов, в столбцах которой нет ни одного дубля. Третью строку мы можем записать n! числом способов. Если из этих n! способов вычесть количество тех, при которых в столбцах таблицы возникнет 1 дубль, 2 дубля,3 дубля,......, n дублей, то останутся те способы, заполнения третьей строки, при которых в таблице не будет ни дублей, ни триплетов. Они и будут беспорядками порядков, представленных в первых двух строках.
при заполнении третьей строки один дубль может возникнуть на любой из n ячеек строки. Т.е. может возникнуть на
Вроде бы рассуждения верные, но компьютерный расчет опровергает этот результат. На самом деле решение раздваивается и зависит не только от n, но и от выбора первых двух строк. Из-за чего может происходить такое раздвоение результатов? Какие ошибки могут быть в приведенных рассуждениях?
Последний раз редактировалось buratino.2016 27 ноя 2019, 18:02, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Олимпиадные задачи»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей