Нетривиальная задача про дубли

buratino.2016

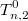
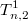
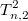
Пусть есть таблица размером n столбцов*2 строки, в каждой строке могут быть записаны в произвольном порядке различные цифры от 1 до n. Каждую возможную запись такой таблицы назовем комбинацией. Если в одном столбце окажется 2-е одинаковые цифры, назовем это дублем. 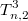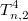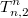Обозначим количество комбинаций, содержащих 0 дублей - $T_{n,2}^0$ , 1 дубль- $T_{n,2}^1$ , 2 дубля - $T_{n,2}^2$ , 3 дубля - $T_{n,2}^3$ , 4 дубля - $T_{n,2}^4$ ,......., n дублей - $T_{n,2}^n$ , где индекс n обозначает, что в таблице n столбцов, а индекс 2 указывает на то, что таблица содержит 2 строки. Верхний индекс i пробегает значения 1-n и символизирует комбинации включающие i дублей.
Очевидно, что количество всех возможных комбинаций заполнения таблицы равно $$(n!)^2$$

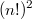
, с другой стороны очевидно, что $\sum_{i=1}^n{T_{n,2}^i}=(n!)^2$
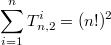
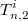
Выразить значения $T_{n,2}^i$ через переменные n,2,i или показать, что это невозможно.
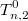
Замечание: $T_{n,2}^0$ равно количеству возможных латинских таблиц, состоящих из 2х строк и n столбцов.

12d3 · Сообщение **12d3** » 28 авг 2016, 17:17

buratino.2016 писал(а):Source of the post Выразить значения T_{n,2}^i через переменные n,2,i или показать, что это невозможно.

$T_{n,2}^i = n! \cdot \binom{n}{i} \cdot !\left ( n-i \right )$ , где $$!a$$

- субфакториал.

buratino.2016

Спасибо, но что-то у меня не сходится с Вашей формулой. Например должно быть $T_{3,2}^0=12,T_{3,2}^1=18,T_{3,2}^2=0,T_{3,2}^3=6$ .
Может я не понял Вашу формулу? Какие значения она дает для этих величин?
По Вашей формуле у меня получилось соответственно: $$3,9,0,6$$

проверка моих значений:
$$12+18+0+6=(3!)^2=36$$

buratino.2016

Извиняюсь, я неправильно посчитал субфакториал. подставил его табличные значения- всё работает, только значения для !0 в таблице не было. Оно не определено? Если не определено, то как искать $T_{n,2}^n?$

Как Вы нашли решение? Не с помощью мат. пакетов случайно?

buratino.2016

И ещё вопрос, что такое $\Gamma (n+1,-1)$ ? То, что это неполная гамма функция я прочел, но неполная сверху или неполная снизу? и почему такое странное обозначение? Что значит -1 после запятой в скобках?

buratino.2016

Нашел, что субфакториал нуля: $$!0=1$$

, что вполне согласуется с представленным решением. Также выяснил, что $\Gamma (n+1,-1)$ - это неполная сверху гамма-функция, где зафиксирован верхний предел интегрирования.

Осталось непонятным как уважаемый 12d3 нашел решение.

buratino.2016

12d3, я понял как Вы решили эту задачу. Вы были знакомы с задачей о беспорядках, далее, первую строку можно записать $$n!$$

способами. С каждым из способов существуют случаи содержащие дубли. $$i$$

дублей можно выбрать $$C_n^i$$

способами. С каждым из способов решается задача о беспорядках для чисел не являющихся дублями, решение дает $$!(n-i)$$

способов. Итого: $n!\cdot!(n-i)C_n^i$ способов. И никакие мат. пакеты не нужны )
С триплетами уже посложнее.
Кстати, Вам просила передать привет Omega, она приглашает Вас на форум: http://mathhelpplanet.com http://mathhelpplanet.com

12d3 · Сообщение **12d3** » 30 авг 2016, 21:57

Да, все верно, только с задачей о беспорядках я ознакомился в момент решения. Омега я тоже передаю привет, но от предложения, пожалуй, откажусь. Разонравились немножко магические квадраты и иже с ними.

yourdomain.com