Putnam 2012
Putnam 2012
А насчет 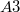 есть идеи по док-ву единственности? Определить бы
есть идеи по док-ву единственности? Определить бы 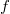 на всюду плотном множестве, но ни на рацинальных ни на числах вида
на всюду плотном множестве, но ни на рацинальных ни на числах вида 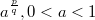 явно значения я указать так и не смог...
явно значения я указать так и не смог...
Последний раз редактировалось xmaister 28 ноя 2019, 15:18, всего редактировалось 1 раз.
Причина: test
Причина: test
Putnam 2012
Не знаю, насколько это строго, но в A3 всегда 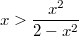 , потому мы можем свести вычисление
, потому мы можем свести вычисление 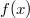 к вычислению
к вычислению  для сколь угодно малого
для сколь угодно малого 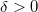 через функциональное соотношение, а
через функциональное соотношение, а  для сколь угодно малого
для сколь угодно малого  , значит мы можем вычислить
, значит мы можем вычислить 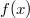 с точностью
с точностью 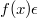 , которая может быть сделана произвольностью
, которая может быть сделана произвольностью 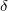 сколь угодно малой.
сколь угодно малой.
Значит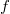 единственна.
единственна.
Ну и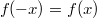 .
.
А вот чему она равна!? Блин!
Значит
Ну и
А вот чему она равна!? Блин!
Последний раз редактировалось Sonic86 28 ноя 2019, 15:18, всего редактировалось 1 раз.
Причина: test
Причина: test
Putnam 2012
Исправил А1, а А5 заменил моим переводом - он почти дословен оригиналу, так как было не до изысков. Начинали мы раньше всех.
Последний раз редактировалось bot 28 ноя 2019, 15:18, всего редактировалось 1 раз.
Причина: test
Причина: test
Putnam 2012
Про B6. Утверждение обобщается так:
Пусть нечетно. Пусть
нечетно. Пусть  - перестановка
- перестановка 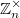 (это будет в точности для всех
(это будет в точности для всех 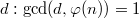 ). Тогда
). Тогда 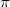 - четная перестановка для всех
- четная перестановка для всех 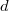
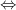 каноническое разложение
каноническое разложение  состоит лишь из простых
состоит лишь из простых  .
.
В случае остальных перестановки м.б. как четны, так и нечетны. Пока не разобрал, что получается в таком случае.
перестановки м.б. как четны, так и нечетны. Пока не разобрал, что получается в таком случае.
(если надо - есть программулина, это все считающая).
upd: Точнее: В остальных случаях имеют место как четные, так и нечетные перестановки, причем перестановок обеих типов одинаковое число.
(это уже означает, что доказательства утверждения в разные стороны будут сильно различны)
upd2: Кажись наврал в формулировке. Надо так: нечетные перестановки есть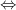 в каноническом разложении
в каноническом разложении  число различных простых вида
число различных простых вида  нечетно.
нечетно.
upd3: Если рассматривать только свободные от квадратов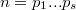 , то четность перестановки
, то четность перестановки  равна сумме четностей перестановок
равна сумме четностей перестановок  .
.
Насчет одинаковости числа нечетных и четных перестановок в том случае, когда они есть: это очевидно: отображение - гомоморфизм
- гомоморфизм 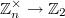 , мощность его ядра равна
, мощность его ядра равна 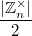 . (кстати группа перестановок коммутативна)
. (кстати группа перестановок коммутативна)
upd4: Если , то для любого
, то для любого  , свободного от квадратов, все перестановки
, свободного от квадратов, все перестановки  четны. В случае
четны. В случае  могут быть как четны, так и нечетны. Случай
могут быть как четны, так и нечетны. Случай 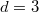 описан, прочие случаи описать пока затрудняюсь.
описан, прочие случаи описать пока затрудняюсь.
(ненужное удалил)
Пусть
В случае остальных
(если надо - есть программулина, это все считающая).
upd: Точнее: В остальных случаях имеют место как четные, так и нечетные перестановки, причем перестановок обеих типов одинаковое число.
(это уже означает, что доказательства утверждения в разные стороны будут сильно различны)
upd2: Кажись наврал в формулировке. Надо так: нечетные перестановки есть
upd3: Если рассматривать только свободные от квадратов
Насчет одинаковости числа нечетных и четных перестановок в том случае, когда они есть: это очевидно: отображение
upd4: Если
(ненужное удалил)
Последний раз редактировалось Sonic86 28 ноя 2019, 15:18, всего редактировалось 1 раз.
Причина: test
Причина: test
Putnam 2012
A1. Пусть числа (не обязательно попарно различные) 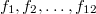 расположены на интервале
расположены на интервале 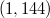 в порядке (нестрогого) возрастания. Покажем, что найдутся три последовательных элемента
в порядке (нестрогого) возрастания. Покажем, что найдутся три последовательных элемента  такие, что
такие, что 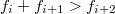 . Действительно, в противном случае будут иметь место неравенства
. Действительно, в противном случае будут иметь место неравенства  ,
,  ,
,
влекущие ,
,  ,
,  ,
,  . Противоречие.
. Противоречие.
Рассмотрим теперь числа на интервале
на интервале 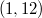 . Из доказанного выше следует, что найдется тройка
. Из доказанного выше следует, что найдется тройка  со свойством
со свойством  , из которого следует, в частности, что
, из которого следует, в частности, что  . Неравенства треугольника для элементов
. Неравенства треугольника для элементов  и
и  выполняются тривиально. Следовательно, по теореме косинусов
выполняются тривиально. Следовательно, по теореме косинусов  являются длинами сторон остроугольного треугольника.
являются длинами сторон остроугольного треугольника.
влекущие
Рассмотрим теперь числа
Последний раз редактировалось fri739 28 ноя 2019, 15:18, всего редактировалось 1 раз.
Причина: test
Причина: test
Putnam 2012
fri739 писал(а):Source of the post
A1. Пусть числа (не обязательно попарно различные)расположены на интервале
в порядке (нестрогого) возрастания. Покажем, что найдутся три последовательных элемента
такие, что
. Действительно, в противном случае будут иметь место неравенства
,
,
влекущие,
,
,
. Противоречие.
Рассмотрим теперь числана интервале
. Из доказанного выше следует, что найдется тройка
со свойством
, из которого следует, в частности, что
. Неравенства треугольника для элементов
и
выполняются тривиально. Следовательно, по теореме косинусов
являются длинами сторон остроугольного треугольника.
Последний раз редактировалось fri739 28 ноя 2019, 15:18, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Олимпиадные задачи»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей