Решить по-русски

Ian · Сообщение **Ian** » 08 ноя 2011, 07:41

BSK писал(а):Source of the post
Пара вопросов:
1) Где база индукции при бесконечном числе квадратиков?

Ну это несложно, мы же доказываем. что существует алгоритм упаковки, что для любого N первые N квадратиков упаковывается. Индукция как раз по N

2) Допустим, можем заложить прямоугольник высоты с уже накрытым куском на (у меня на ) не менее чем наполовину. Что дальше, как решать исходную задачу про то, как вместить в квадрат все маленькие квадратики?

А тут действительно проблемы. Например, 12 квадратиков со стороной 0.2 в уголок уже не влезут. Но проблемы общие, я не вижу, как это у Вас решалось. Например, чему у Вас окажется равно Н: 0,8 или 0,2?

BSK · Сообщение **BSK** » 08 ноя 2011, 07:55

Ian писал(а):Source of the post
BSK писал(а):Source of the post
Пара вопросов:
1) Где база индукции при бесконечном числе квадратиков?
Ну это несложно, мы же доказываем. что существует алгоритм упаковки, что для любого N первые N квадратиков упаковывается. Индукция как раз по N
2) Допустим, можем заложить прямоугольник высоты с уже накрытым куском на (у меня на ) не менее чем наполовину. Что дальше, как решать исходную задачу про то, как вместить в квадрат все маленькие квадратики?
А тут действительно проблемы. Например, 12 квадратиков со стороной 0.2 в уголок уже не влезут. Но проблемы общие, я не вижу, как это у Вас решалось. Например, чему у Вас окажется равно Н: 0,8 или 0,2?

С индукцией непонятно. Если число квадратиков конечно, то для размещения квадратиков во вложенном прямоугольнике имеется меньше квадратиков, потом ещё меньше и т.д. Т.е. базовым утверждением является возможность поместить в прямоугольник 1 квадратик. При бесконечном числе квадратиков неиспользованных остается всегда бесконечное число.

Проблемы не общие. Я доказываю, что могу замостить уголок не менее чем наполовину. В результате свожу задачу к размещению оставшихся квадратиков вне уголка, т.е. снова внутри квадрата (только с уже меньшим числом неиспользованных квадратиков).

Я помещаю в левый нижний угол самый крупный квадратик (Н равно его стороне). Затем заполняю прямоугольники справа и сверху от него.

Ian · Сообщение **Ian** » 08 ноя 2011, 11:10

BSK писал(а):Source of the post
Ian писал(а):Source of the post
BSK писал(а):Source of the post
Пара вопросов:
1) Где база индукции при бесконечном числе квадратиков?
Ну это несложно, мы же доказываем. что существует алгоритм упаковки, что для любого N первые N квадратиков упаковывается. Индукция как раз по N
2) Допустим, можем заложить прямоугольник высоты с уже накрытым куском на (у меня на ) не менее чем наполовину. Что дальше, как решать исходную задачу про то, как вместить в квадрат все маленькие квадратики?
А тут действительно проблемы. Например, 12 квадратиков со стороной 0.2 в уголок уже не влезут. Но проблемы общие, я не вижу, как это у Вас решалось. Например, чему у Вас окажется равно Н: 0,8 или 0,2?

С индукцией непонятно. Если число квадратиков конечно, то для размещения квадратиков во вложенном прямоугольнике имеется меньше квадратиков, потом ещё меньше и т.д. Т.е. базовым утверждением является возможность поместить в прямоугольник 1 квадратик. При бесконечном числе квадратиков неиспользованных остается всегда бесконечное число.

Пользуемся тем, что Ваш процесс не зависит от хвоста убывающей последовательности квадратиков, значит, и от того, конечен он или бесконечен."Бесконечно убывающая последовательность упакована"=про каждый N-й сказано, куда он упакован. А у Вас сказано, потому что упаковка последовательности $$a_1>a_2>...>a_n$$

служит началом упаковки последовательности $a_1>a_2>...>a_n>a_{n+1}$ , значит каждому квадратику определено корректное место.

Проблемы не общие. Я доказываю, что могу замостить уголок не менее чем наполовину.

Вот это у меня было нечетко, получилось, что любая полка уголка, объединенная с угловым, заполнена на >50%, но отсюда не следует, что весь уголок заполнен на >50%

В результате свожу задачу к размещению оставшихся квадратиков вне уголка, т.е. снова внутри квадрата (только с уже меньшим числом неиспользованных квадратиков).

Я помещаю в левый нижний угол самый крупный квадратик (Н равно его стороне). Затем заполняю прямоугольники справа и сверху от него.

Ну я поправлю в крайнем случае завтра, все равно можно избежать упоминания красных квадратиков (т.к. не понял описания) и пунктира (т.к. он мешает "оптимальности упаковки")

Ув. участники. А что с задачей 7 (4 поста назад)? На AoPS ее то ли забыли, то ли не поняли. А вроде понятна и решаема?

BSK · Сообщение **BSK** » 08 ноя 2011, 11:23

Ian писал(а):Source of the post Пользуемся тем, что Ваш процесс не зависит от хвоста убывающей последовательности квадратиков, значит, и от того, конечен он или бесконечен."Бесконечно убывающая последовательность упакована"=про каждый N-й сказано, куда он упакован. А у Вас сказано, потому что упаковка последовательности служит началом упаковки последовательности $a_1>a_2>...>a_n>a_{n+1}$ , значит каждому квадратику определено корректное место.

Вопрос не про то, можно ли упаковать бесконечную последовательность. А про индукцию в бесконечном случае.

Ian · Сообщение **Ian** » 09 ноя 2011, 17:33

Вот это место нуждалось в исправлении:

Ian писал(а):Source of the post Док-во.Процесс и рисунок Ваши: понятно как располагаем, рядом, сначала пробуем над ним, если невозможно, то рядом. Если возможно, рекурсия. В итоге сторона исходного прямоугольника длиной В разобьется на некоторое количество m отрезков- сторон квадратиков и (m+1)-й отрезок короче чем $a_{k+1}$ .По предположению индукции для прямоугольников длиной А, а ширинами равными 2му,...m-му отрезкам, расположенные в них квадратики занимают не менее 50% их площади. А в 1-м и (m+1)м прямоугольниках, вместе взятых, составляет не менее 50% площади.

Поправлю, в двух местах еще приблизившись по форме к решению BSK: $a_1=H,a_2=h\leqslant H$ так соответствуют наши обозначения. В цитате я показывал, что можно заложить прямоугольник $1\times H$ не менее чем на 50% площади. А надо было - что можно заложить уголок $(1-H)\times H+H\times H+(1-H)\times H$ . В предположении $H^2+h^2<\frac 12$ , все-таки оно нужно, $$H+h<1,h<1-H$$

и второй квадратик помещается в полку уголка не только по ее ширине Н, но и по длине. В итоге сторона исходного прямоугольника длиной 1 разобьется на некоторое количество m>1 отрезков- сторон квадратиков и (m+1)-й отрезок короче чем $$h$$

. Уберем половину первого отрезка из стороны, и покажем, что $(1-\frac H2)\times H$ закрыт не менее чем наполовину. Связный кусок с основанием= объединению 3го,...m-го отрезков либо пуст, либо покрыт не менее чем наполовину, по построению. Остается площадь над отрезками 1) $\frac H2$ , 2) $$h$$

,m+1)

высотой Н, $\frac{H^2}2$ и $$h^2$$

в сумме покрывают более половины ее, т.к. $\frac{H^2}2+h^2\geqslant 0,5H(\frac H2+2h)$ всегда( а я-то думал, зачем в самом 1м изложении BSK было это неравенство!). Другую половину уголка покрываем после этого тоже не менее чем наполовину, и индукционный переход к меньшему квадрату и меньшему набору.
По сути, здесь двойная рекурсия ( рекурсивный алгоритм заполнения полок вложен в рекурсивный алгоритм отбрасывания уголков) и соответственно двойная индукция, так что упрощать вряд ли выйдет.

Задача 7 - в том же состоянии

BSK · Сообщение **BSK** » 11 ноя 2011, 10:54

Ian писал(а):Source of the post Дана таблица n*n.
........................................
Может ли оказаться, что B>A?

Не может.

слагаемое суммы $$A$$

(

) не меньше $b_{n+1-k}$ слагаемого суммы $$B$$

потому, что $$a_k$$

является наибольшим числом в таблице $$(n+1-k)*(n+1-k),$$

а $b_{n+1-k}$ - наименьшим числом в таблице $$k*k,$$

которые имеют общий элемент.

Ian · Сообщение **Ian** » 19 ноя 2011, 13:21

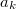
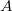
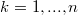
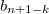
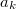
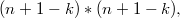
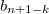
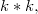
BSK писал(а):Source of the post слагаемое суммы () не меньше $b_{n+1-k}$ слагаемого суммы потому, что является наибольшим числом в таблице а $b_{n+1-k}$ - наименьшим числом в таблице которые имеют общий элемент.

действительно, дополнение к пересечению таблиц размером $(n+1-k)\times (n+1-k)$ и $k\times k$ можно получать, выкинув n-k+1 столбцов, а потом еще k, различных столбцов будет выкинуто не более n-1, значит, хоть один останется. Потом так же выкинуть строки, и хоть один элемент останется.

Не всегда мне нравится все что я там вижу, но вот тут можно развить идеи решения задачи 4б), а они были хороши:

8..Доказать, что квадраты со сторонами $1,\frac 12,\frac 13,\frac 14,\frac 15...$ могут быть размещены без пересечений в квадрате со стороной $\frac 32$ .
Без пересечений -как и прежде, означает, что никакие 2 квадратика из набора не имеют общей внутренней точки. Общую точку границ иметь могут.
Задача "горячая", стоит посматривать на пост-оригинал (щелкнуть по номеру

UPD Там решена, говорил же горячая. Где-то 5:2:)
Вот тоже горячая, и даже близка к учебной.
9. Доказать, что не существует всюду дифференцируемой функции f(x), такой что
$\displaystyle f(x)+f'(x)=$ $\displaystyle \\\sin x, if\ x\leqslant 0\\\cos x, if\ x>0$

Видно как минимум два пути, интересно, какой выберете

Ian · Сообщение **Ian** » 24 ноя 2011, 17:12

Ian писал(а):Source of the post
9. Доказать, что не существует всюду дифференцируемой функции f(x), такой что
$\displaystyle f(x)+f'(x)=$ $\displaystyle \\\sin x, if\ x\leqslant 0\\\cos x, if\ x>0$

"мехматовское" решение: функция f непрерывна, значит, точку разрыва 1го рода в нуле имеет производная. А для функции, дифференцируемой в каждой точке, производная не может иметь разрыв 1го рода.
=====
Полчаса уже не дается задачка:
10.Функция $f:\mathbb R \to\mathbb R$ , не равна нулю тождественно. Известно, что при любых х,у $$f(x)+xf(y)$$

лежит в образе функции f (то есть существует z, что $$f(x)+xf(y)=f(z)$$

). Можно ли утверждать, что образ f - вся $\mathbb R$ ?

Ian · Сообщение **Ian** » 27 ноя 2011, 17:29

10 блестяще решена недавно, см. по ссылке и контрпример таков:
$$f(x)=$$

$\displaystyle \\x-1,x\ne 0\\0,x=0$

Вот спросили там срочно в Private Message (нас уже читают, даже русским не владея), за полчаса не вышла, помогите.
11.Дан простой граф , все вершины которого имеют порядок не менее трех. Доказать, что существует простой (без повторения вершин) цикл длины, не делящейся на 3.

Ian · Сообщение **Ian** » 26 дек 2011, 13:12

Вот эту очень захотелось перевести. Запостили сутки назад, 38 просмотров, на 4й странице таблицы Unanswered posts, значит кто-то еще думает но не придумал, а остальные мало кто посмотрит. Вся надежда на вас

12. По кругу равномерно расположены 12 домиков. 4 человека A,B,C,D занимают некоторые 4 домика по часовой стрелке, а остальные домики пусты. За один ход один человек может переместиться в домик, расположенный через 4 пятым от занимаемого им (в общем, на 5/12 окружности), по часовой стрелке или против, но если домик пустует.
После нескольких ходов оказалось, что эти 4 человека снова занимают 4 соседних домика. В каком порядке по часовой стрелке они могут расположиться?

Всего порядков может быть 12 от ABCD до DCBA, надо среди них отметить какие возможны

yourdomain.com