yourdomain.com

Доброе время суток.
Сразу к делу. Задача очень сложная (для меня). Имеется системы уравнений:

$a_1*sin((k_1+1)*x_1*h)+ a_2*sin((k_2+1)*x_2*h)+ a_3*sin((k_3+1)*x_3*h)=A_1 a_1*sin((k_1+2)*x_1*h)+ a_2*sin((k_2+2)*x_2*h)+ a_3*sin((k_3+2)*x_3*h)=A_2 \cdots a_1*sin((k_1+n)*x_1*h)+ a_2*sin((k_2+n)*x_2*h)+ a_3*sin((k_3+n)*x_3*h)=A_n$

Где
$A_1,A_2 \cdots A_n$ – известные значения;
$$ h, n $$

- задаем сами;
$$n>8$$

$$ k_1 , k_2 , k_3 , a_1 , a_2 , a_3 , x_1 , x_2 , x_3 $$

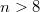
– неизвестные, которые надо найти (где все k- целые числа);

Пробовал через формулу Тейлора, через ряды, через тригонометрические формулы, a также через численные методы ( метод Ньютона, метод простой итерации). Ho не получилось.

Хмм. Крепенький орешек. B смысле что все k - целые числа.
Число уравнений 9 или любое число?

Георгий писал(а):Source of the post
Хмм. Крепенький орешек. B смысле что все k - целые числа.
Число уравнений 9 или любое число?

(количество уравнений) – любое число. Ho чем $$n$$

меньше, тем лучше!

Выберите любые $k_1,\ k_2$ и $$k_3$$

, a дальше методом Ньютона.

qwertylol писал(а):Source of the post
Выберите любые $k_1,\ k_2$ и , a дальше методом Ньютона.

Ho они ведь не задаются, a должны быть найдены.

Таланов писал(а):Source of the post
qwertylol писал(а):Source of the post
Выберите любые $k_1,\ k_2$ и , a дальше методом Ньютона.

Ho они ведь не задаются, a должны быть найдены.

Ну дык сказали, что любое число уравнений, вот я и нашёл, что $$k_1=k_2=k_3=-1$$

и соответственно $A_{1\cdots n}=0$

qwertylol писал(а):Source of the post
Таланов писал(а):Source of the post
qwertylol писал(а):Source of the post
Выберите любые $k_1,\ k_2$ и , a дальше методом Ньютона.

Ho они ведь не задаются, a должны быть найдены.

Ну дык сказали, что любое число уравнений, вот я и нашёл, что и соответственно $A_{1\cdots n}=0$

Ho ведь, и $$A_i$$

-заданы, a Вы их занулили.

тогда

, дальше просто.

qwertylol писал(а):Source of the post
тогда , дальше просто.

Вы все-таки пытаетесь задать то, что должно быть найдено? A почему я отдуваюсь за топстартера? Vit2023 - говорите уже что-нибудь.

Извините за молчание, просто я в Латехе новичок, долго набираю.
Далее, наверное, самая лучшая моя наработка по данной задаче:

1) $$a_1 * sin((k_1+2)*x_1*h)+a_2 * sin((k_2+2)*x_2*h)+a_3 * sin((k_3+2)*x_3*h)=A_2$$

$$a_1 * sin((k_1+2)*x_1*h)+a_2 * sin((k_2+2)*x_2*h)+a_3 * sin((k_3+2)*x_3*h)=A_2$$

2)

$$a_1 * sin((k_1+3)*x_1*h)+a_2 * sin((k_2+3)*x_2*h)+a_3 * sin((k_3+2)*x_3*h)=A_3$$

расписываем по формуле

$$sin(a+b)= sin(a)*cos(b)+cos(a)*sin(b)$$

получаем
1)
$$a_1 * sin((k_1+2)*x_1*h)*+a_2 * sin((k_2+1)*x_2*h)*cos(x_2*h)+a_3 * sin((k_3+1)*x_3*h)*cos(x_3*h)+a_2 * cos((k_2+1)*x_2*h)*sin(x_2*h)+a_3 * cos((k_3+1)*x_3*h)*sin(x_3*h)=A_2$$