Ну, теперь, эта..., ну теперь...!
Главные центральные моменты инерции треугольника масс
Главные центральные моменты инерции треугольника масс
Спасибо ARRY, получилось!
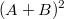
Ну, теперь, эта..., ну теперь...!
Ну, теперь, эта..., ну теперь...!
Последний раз редактировалось Anik 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
Далее, буду руководствоваться упомянутой книгой Ефимова: "Квадратичные формы и матрицы".
Приведение квадратичной формы к каноническому виду связано с решением характеристического уравнения:

Корни этого уравнения:

Вспомним, что

Поскольку взаимное расположение точек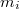 задано, то можно считать, что нам известны векторы
задано, то можно считать, что нам известны векторы 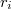 , и углы между этими векторами.
, и углы между этими векторами.
Выберем направление оси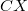 по вектору
по вектору 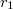 (см. рис.), ось
(см. рис.), ось 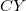 направим перпендикулярно оси
направим перпендикулярно оси 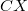 , и найдём моменты инерции треугольника в этой системе координат.
, и найдём моменты инерции треугольника в этой системе координат.




В выражение для корней характеристического уравнения входит величина:
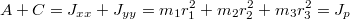
Это полярный момент инерции треугольника. Ещё входит величина:

(Поправил.)
Здесь я для краткости обозначил через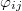 угол между соответствующими векторами
угол между соответствующими векторами 
Теперь, подсчитаем подкоренное выражение:
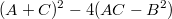
Я решил отправить это сообщение, прежде чем считать дальше, а то у меня компьютер шизует и набранные ответы пропадают, приходится снова набирать, запарился уже!
Приведение квадратичной формы к каноническому виду связано с решением характеристического уравнения:
Корни этого уравнения:
Вспомним, что
Поскольку взаимное расположение точек
Выберем направление оси

В выражение для корней характеристического уравнения входит величина:
Это полярный момент инерции треугольника. Ещё входит величина:
(Поправил.)
Здесь я для краткости обозначил через
Теперь, подсчитаем подкоренное выражение:
Я решил отправить это сообщение, прежде чем считать дальше, а то у меня компьютер шизует и набранные ответы пропадают, приходится снова набирать, запарился уже!
Последний раз редактировалось Anik 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
Продолжу,
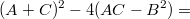
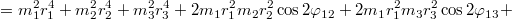
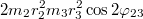
Подставляя это выражение под квадратный корень, мы найдём корни характеристического уравнения
Но, нам нужно найти угол между осью
между осью 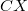 и осью
и осью  новой, канонической системы координат. Для этого нужно найти направляющие косинусы новой оси
новой, канонической системы координат. Для этого нужно найти направляющие косинусы новой оси 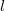 и
и  . Их можно найти из системы (11), (см. Ефимова на стр.13)
. Их можно найти из системы (11), (см. Ефимова на стр.13)

Вместо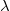 можно подставить один из найденных корней характеристического уравнения.
можно подставить один из найденных корней характеристического уравнения.
Угол найдётся из формулы:
найдётся из формулы:

Продолжу завтра.
Подставляя это выражение под квадратный корень, мы найдём корни характеристического уравнения
Но, нам нужно найти угол
Вместо
Угол
Продолжу завтра.
Последний раз редактировалось Anik 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
Заметим, что дискриминант  , поэтому имеем два разных или кратных корня. Этот дискриминант легче запомнить если представить себе формулу для
, поэтому имеем два разных или кратных корня. Этот дискриминант легче запомнить если представить себе формулу для 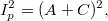 только "испорченную" косинусами двойных углов. Дискриминант равен нулю в случае равностороннего треугольника, у которого углы между радиус-векторами
только "испорченную" косинусами двойных углов. Дискриминант равен нулю в случае равностороннего треугольника, у которого углы между радиус-векторами  равны
равны 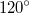 и равны сами векторы (по модулю) и массы точек. В этом можно убедиться, подставляя эти значения в формулу, которую получили в предыдущем посте. В этом случае корень один (кратный) и все направления - главные.
и равны сами векторы (по модулю) и массы точек. В этом можно убедиться, подставляя эти значения в формулу, которую получили в предыдущем посте. В этом случае корень один (кратный) и все направления - главные.
Итак, мы нашли:

Здесь и
и 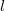 - направляющие косинусы некоторого вектора, лежащего на одном из главных направлений (в зависимости от выбранного корня
- направляющие косинусы некоторого вектора, лежащего на одном из главных направлений (в зависимости от выбранного корня 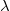 ).
).
Если потребовать чтобы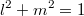 , то этот направляющий вектор будет единичным, а решение системы (11) - нормированным.
, то этот направляющий вектор будет единичным, а решение системы (11) - нормированным.

Итак, мы нашли:
Здесь
Если потребовать чтобы
Последний раз редактировалось Anik 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
Решение.
Пусть точки имеют массы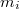 и координаты
и координаты  . Координаты центра масс
. Координаты центра масс 
 . Переместим начало координат в центр масс. Координаты точек станут
. Переместим начало координат в центр масс. Координаты точек станут  .
.
Повернем все точки на угол вокруг нового начала координат. Новые координаты точек будут равны
вокруг нового начала координат. Новые координаты точек будут равны  .
.
Приравняем центробежный момент инерции к нулю.





Вот и ответ.
Пусть точки имеют массы
Повернем все точки на угол
Приравняем центробежный момент инерции к нулю.
Вот и ответ.
Последний раз редактировалось 12d3 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
Вот здорово! Ставлю вам +
Всё гениальное просто!
Всё гениальное просто!
Последний раз редактировалось Anik 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
В формуле:

можно вынести двойку в числителе за знак суммы, получим:

Теперь заметим, что в числителе центробежный момент относительно оси, лежащей в плоскости фигуры, а в знаменателе - разность моментов инерции всех точек фигуры относительно оси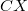 и
и 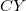 . С учётом этого, формулу можно записать так:
. С учётом этого, формулу можно записать так:

Если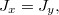 то
то 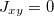 . и мы получим 0/0. В этом случае все оси главные и угол
. и мы получим 0/0. В этом случае все оси главные и угол  потеряет смысл.
потеряет смысл.
Я ничего не накосячил?
можно вынести двойку в числителе за знак суммы, получим:
Теперь заметим, что в числителе центробежный момент относительно оси, лежащей в плоскости фигуры, а в знаменателе - разность моментов инерции всех точек фигуры относительно оси
Если
Я ничего не накосячил?
Последний раз редактировалось Anik 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
За знак суммы можно, а за знак арктангенса - нельзя. Верните двойки. Если вернете, то все остальное с моментами инерции верно.Anik писал(а):Source of the post можно вынести двойку в числителе за знак суммы, получим:
Последний раз редактировалось 12d3 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
Нет, так тоже нельзя. Оставьте одну вторую перед арктангенсом, а двойку внутри арктангенса.
Последний раз редактировалось 12d3 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Главные центральные моменты инерции треугольника масс
А если так
:
Теперь двойку можно сократить? Чтобы получить:

***Простите, я здесь не прав! Дело в том, что мы нашли тангенс двойного угла, поэтому нужно взять половину арктангенса. Нужно было написать вместо (*)

:
Теперь двойку можно сократить? Чтобы получить:
***Простите, я здесь не прав! Дело в том, что мы нашли тангенс двойного угла, поэтому нужно взять половину арктангенса. Нужно было написать вместо (*)
Последний раз редактировалось Anik 27 ноя 2019, 17:53, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Другие разделы математики»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость