Диаграммы Эйлера-Венна

Andrew58 · Сообщение **Andrew58** » 06 фев 2012, 16:28

BIOSonar писал(а):Source of the post
Ну ошибка не столь важна. Я понял что вариант с подстановкой готовых изображений - чушь полная, слишком нелепо из-за такого большого количества изображений для приложения, даже если навскидку.
Спасибо всем.

Насколько я понимаю, верхней оценкой может служить $$2^4=16$$

. Если это "много", то я искренне сочувствую математикам.

Hottabych · Сообщение **Hottabych** » 06 фев 2012, 16:30

областей на диаграмме Эйлера-Вена для трех множеств. Каждая из этих 8 областей может быть закрашена. Итого получаем $$2^8$$

диаграмм.

Sonic86 · Сообщение **Sonic86** » 06 фев 2012, 16:38

Наверное, можно так: пусть дано множество $$M$$

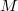
из

элементов $\{ A_1,...,A_n\}$ (у нас $$n=3$$

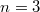
). Мы берем множество $$P_n$$

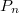
всех подмножеств данного множества - в нем $$2^n$$

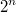
элементов и в нем же берем отношение включения - частичного порядка. Нам нужно задать в $$P_n$$

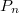
2 подмножества специального типа (не знаю, как они называются), назовем их полные по иерархии - одно полное по иерархии, второе - по антииерархии.
Наша диаграмма будет полностью определяться корректным заданием все пустых пересечений подмножеств из $$M$$

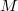
и всех полных объединений подмножеств из $$M$$

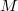
. Подмножеству из $$M$$

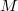
биективно соответствует элемент $$P_n$$

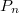
. Так что нам надо задать все пустые элементы (обозначим их множество $$N$$

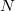
) из

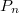
и все "полные" (т.е. совпадающие с универсальным множеством $$U$$

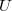
) элементы (обозначим их множество $$A$$

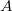
). Но просто так их задать нельзя (т.е. нельзя выбрать произвольное подмножество из $$P_n$$

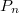
) - для их задания необходимо (и достаточно) учесть условия $X \subset \varnothing \Rightarrow X = \varnothing$ и двойственное $U \subset X \Rightarrow X=U$ . Если бы мы выбирали просто подмножества $$P_n$$

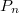
- получилось бы только для $$N$$

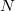
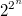
много - $2^{2^n}$ . А с условием корректности: $(\exists y \in N)y \leqslant x \Rightarrow y \in N$ их будет немного меньше. Кстати сколько? Для $$n=3$$

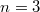
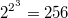
$2^{2^3}=256$ , а множеств $$N$$

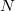
всего

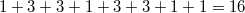
(или наврал? если не наврал, то 16 - это красивое число!). Вот пусть их число $$C_n$$

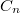
. Тогда независимых выборов $$N,A$$

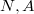
будет

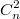
и еще надо учесть условие $N \subset A$ , поскольку $\varnothing \subset U$ - получится немного меньше, чем $$C_n^2$$

.
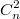
Хотя бы так попробовать (руками для $$n=3$$

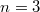
перебрать вполне реально).
И еще хорошо бы симметрию учесть - но это трудно.
Извините за поток слов

BIOSonar · Сообщение **BIOSonar** » 06 фев 2012, 17:07

Никак не может быть 16 рисунков.

Andrew58 · Сообщение **Andrew58** » 06 фев 2012, 17:11

Hottabych писал(а):Source of the post
областей на диаграмме Эйлера-Вена для трех множеств. Каждая из этих 8 областей может быть закрашена. Итого получаем диаграмм.

Мне немного непонятно, учитывается ли здесь, что А+В, к примеру, тоже область, которую надо покрасить другим цветом. И она может пересекаться с С куском А или куском В или всеми вместе...

BIOSonar писал(а):Source of the post
Никак не может быть 16 рисунков.

Я говорил только о верхней оценке.

vicvolf · Сообщение **vicvolf** » 06 фев 2012, 19:02

Hottabych писал(а):Source of the post
областей на диаграмме Эйлера-Вена для трех множеств.

На основании формулы включений и исключений для трех множеств имеем 7 областей на диаграмме Эйлера-Венна. Если каждая из областей является подмножеством множества диаграмм, то всего диаграмм $$2^7=128$$

. В этом случае, различные записи тождественных выражений (в смысле сообщения 7) не считаются.

myn · Сообщение **myn** » 07 фев 2012, 13:22

Hottabych писал(а):Source of the post
областей на диаграмме Эйлера-Вена для трех множеств. Каждая из этих 8 областей может быть закрашена. Итого получаем диаграмм.

+1

8 областей , каждая из них может пребывать в одном из двух состояний: закрашено/не закрашено. Так что $$2^8=256$$

.

В самом общем случае (когда события не входят в другие) не пересекающихся областей 8:
- три области только А, В и С
- три области - пересечения двоек - АВ, АС и ВС
- одна область - все три АВС
- всё вне трех событий.

vicvolf · Сообщение **vicvolf** » 07 фев 2012, 13:45

myn писал(а):Source of the post
- всё вне трех событий.

+1 Да, верно!

yourdomain.com